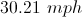Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Understanding Polynomial Functions

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Understanding Polynomial Functions

It took Jack 25 minutes to travel 14 miles, what was Jack's average speed in mph?

Possible Answers:

$2.4\ mph$ $\displaystyle 2.4\ mph$

$1.78\ mph$ $\displaystyle 1.78\ mph$

$30.21\ mph$ $\displaystyle 30.21\ mph$

$33.6\ mph$ $\displaystyle 33.6\ mph$

Correct answer:

$33.6\ mph$ $\displaystyle 33.6\ mph$

Explanation:

$speed=\frac{distance}{time}$ $\displaystyle speed=\frac{distance}{time}$

$speed=\frac{14\ miles}{25\ minutes }$ $\displaystyle speed=\frac{14\ miles}{25\ minutes }$

* We have to change the time from minutes to hours, there are 60 minutes in one hour.

$speed= \frac{14\ miles}{25\ minutes} * \frac{60\ minutes}{1\ hour}$ $\displaystyle speed= \frac{14\ miles}{25\ minutes} * \frac{60\ minutes}{1\ hour}$

$speed= 33.6\ mph$ $\displaystyle speed= 33.6\ mph$

Report an Error

Example Question #2 : Understanding Polynomial Functions

Let $f(x)=3x^{2}-2$ $\displaystyle f(x)=3x^{2}-2$ and $\displaystyle g(x)= x+2$. Evaluate f(g(3)) $\displaystyle f(g(3))$.

Possible Answers:

$\displaystyle 89$

$\displaystyle 54$

$\displaystyle 27$

$\displaystyle 73$

108 $\displaystyle 108$

Correct answer:

$\displaystyle 73$

Explanation:

Substitute $\displaystyle 3$ into g(x) $\displaystyle g(x)$, and then substitute the answer into f(x) $\displaystyle f(x)$.

$\displaystyle g(x)= x+2$

$\displaystyle g(3)=3+2=5$

$f(x)= 3x^{2}-2$ $\displaystyle f(x)= 3x^{2}-2$

$f(5) =3(5)^{2}-2= 75 -2 = 73$ $\displaystyle f(5) =3(5)^{2}-2= 75 -2 = 73$

Report an Error

Example Question #2 : Understanding Polynomial Functions

Solve the following system of equations:

$\displaystyle -x-3y= 4$

2x+5y=7 $\displaystyle 2x+5y=7$

Possible Answers:

$\left ( 1,-5 \right )$ $\displaystyle \left ( 1,-5 \right )$

Infinite solutions.

$\left ( 2,4 \right )$ $\displaystyle \left ( 2,4 \right )$

$\left ( 41,-15 \right )$ $\displaystyle \left ( 41,-15 \right )$

$\left ( -4,10 \right )$ $\displaystyle \left ( -4,10 \right )$

Correct answer:

$\left ( 41,-15 \right )$ $\displaystyle \left ( 41,-15 \right )$

Explanation:

We will solve this system of equations by Elimination. Multiply both sides of the first equation by 2, to get:

$\displaystyle -2x-6y=8$

Then add this new equation, to the second original equation, to get:

-y = 15 $\displaystyle -y = 15$

y=-15 $\displaystyle y=-15$

Plugging this value of $\displaystyle y$ back into the first original equation, gives:

$\displaystyle -x-3(-15) = 4$

$\displaystyle -x = 4- 45$

x = 41 $\displaystyle x = 41$

Report an Error

View Tutors

Owen
Certified Tutor

CUNY Brooklyn College, Bachelor of Science, Biology, General.

View Tutors

Onyinyechi
Certified Tutor

Imo State University, Nigeria, Bachelor in Arts, Mass Communications. Alabama A & M University, Masters in Education, Element...

View Tutors

Alexa
Certified Tutor

Michigan State University, Bachelor of Science, Nutrition Sciences.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ACT Tutors in Boston, GMAT Tutors in San Francisco-Bay Area, Calculus Tutors in Los Angeles, SAT Tutors in San Diego, ISEE Tutors in Los Angeles, Math Tutors in Atlanta, ISEE Tutors in Dallas Fort Worth, Computer Science Tutors in Los Angeles, SAT Tutors in New York City, GRE Tutors in San Francisco-Bay Area

Popular Courses & Classes

Spanish Courses & Classes in Phoenix, LSAT Courses & Classes in Boston, GRE Courses & Classes in Boston, GRE Courses & Classes in Washington DC, ISEE Courses & Classes in Atlanta, SSAT Courses & Classes in San Francisco-Bay Area, SSAT Courses & Classes in New York City, MCAT Courses & Classes in Miami, LSAT Courses & Classes in Miami, SSAT Courses & Classes in Denver

Popular Test Prep

LSAT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Dallas Fort Worth, SSAT Test Prep in Washington DC, GRE Test Prep in Denver, ACT Test Prep in Boston, SSAT Test Prep in Philadelphia, GRE Test Prep in Houston, SSAT Test Prep in Phoenix, GMAT Test Prep in Washington DC, LSAT Test Prep in Boston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Understanding Polynomial Functions

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : Understanding Polynomial Functions

Example Question #2 : Understanding Polynomial Functions

Example Question #2 : Understanding Polynomial Functions

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: