All High School Math Resources
Example Questions
Example Question #31 : Functions And Graphs
It took Jack 25 minutes to travel 14 miles, what was Jack's average speed in mph?
* We have to change the time from minutes to hours, there are 60 minutes in one hour.
Example Question #394 : Algebra Ii
Let 


Substitute 




Example Question #395 : Algebra Ii
Solve the following system of equations:
Infinite solutions.
We will solve this system of equations by Elimination. Multiply both sides of the first equation by 2, to get:
Then add this new equation, to the second original equation, to get:
or
Plugging this value of 
or
Example Question #1 : Transformations Of Polynomial Functions
List the transformations that have been enacted upon the following equation:
vertical compression by a factor of 4
horizontal stretch by a factor of 6
vertical translation 7 units down
horizontal translation 3 units right
vertical stretch by a factor of 4
horizontal compression by a factor of 6
vertical translation 7 units down
horizontal translation 3 units right
vertical stretch by a factor of 4
horizontal compression by a factor of 6
vertical translation 7 units down
horizontal translation 3 units left
vertical stretch by a factor of 1/4
horizontal compression by a factor of 1/6
vertical translation 7 units down
horizontal translation 3 units right
vertical stretch by a factor of 4
horizontal stretch by a factor of 6
vertical translation 7 units down
horizontal translation 3 units right
vertical stretch by a factor of 4
horizontal compression by a factor of 6
vertical translation 7 units down
horizontal translation 3 units right
Since the equation given in the question is based off of the parent function 

- If
is greater than 1, the function has been vertically stretched (expanded) by a factor of
.
- If
is between 0 and 1, the function has been vertically compressed by a factor of
.
In this case, 

- If
is greater than 1, the function has been horizontally compressed by a factor of
.
- If
is between 0 and 1, the function has been horizontally stretched (expanded) by a factor of
.
In this case, 

- If
is positive, the function was translated
units right.
- If
is negative, the function was translated
units left.
In this case, 

- If
is positive, the function was translated
units up.
- If
is negative, the function was translated
units down.
In this case, 
All High School Math Resources


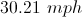

























![f(x)=4[6(x-3)]^{4}-7](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/106187/gif.latex)
![g(x) = a[b(x-c)^{4}]+d](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/106188/gif.latex)



