All High School Math Resources
Example Questions
Example Question #73 : Triangles
One leg of a triangle measures 12 inches. Which of the following could be the length of the other leg if the hypotenuse is an integer length?
By the Pythagorean Theorem, if 



Set 
We can now substitute each of the five choices for 






The only value of 

Example Question #51 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

Find the perimeter of the polygon.
Divide the shape into a rectangle and a right triangle as indicated below.

Find the hypotenuse of the right triangle with the Pythagorean Theorem, 



This is our missing length.
Now add the sides of the polygon together to find the perimeter:
Example Question #41 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem
The lengths of the sides of a right triangle are consecutive integers, and the length of the shortest side is 

Since the lengths of the sides are consecutive integers and the shortest side is 



We then use the Pythagorean Theorem:
Example Question #61 : Triangles
Square 






Quantity A:
Quantity B: The distance between points 
The relationship cannot be determined from the information provided.
The two quantities are equal.
Quantity A is greater.
Quantity B is greater.
The two quantities are equal.
To find the distance between points 



Example Question #11 : Apply The Pythagorean Theorem To Find The Distance Between Two Points In A Coordinate System: Ccss.Math.Content.8.G.B.8
Justin travels 

This is solving for the hypotenuse of a triangle. Using the Pythagorean Theorem, which says that 

Example Question #53 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem
Susie walks north from her house to a park that is 30 meters away. Once she arrives at the park, she turns and walks west for 80 meters to a bench to feed some pigeons. She then walks north for another 30 meters to a concession stand. If Susie returns home in a straight line from the concession stand, how far will she walk from the concession stand to her house, in meters?
25
200
100
50
70
100
Susie walks 30 meters north, then 80 meters west, then 30 meters north again. Thus, she walks 60 meters north and 80 meters west. These two directions are 90 degrees away from one another.
At this point, construct a right triangle with one leg that measures 60 meters and a second leg that is 80 meters.
You can save time by using the 3:4:5 common triangle. 60 and 80 are 


We can solve for the length of the missing hypotenuse by applying the Pythagorean theorem:
Substitute the following known values into the formula and solve for the missing hypotenuse: side 
Susie will walk 100 meters to reach her house.
Example Question #52 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem
The lengths of the sides of a triangle are consecutive odd numbers and the triangle's perimeter is 57 centimeters. What is the length, in centimeters, of its longest side?
23
21
17
25
19
21
First, define the sides of the triangle. Because the side lengths are consecutive odd numbers, if we define the shortest side will be as 
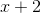

Substitute in the known values and variables.
Subtract 6 from both sides of the equation.
Divide both sides of the equation by 3.
Solve.
This is not the answer; we need to find the length of the longest side, or 
Substitute in the calculated value for 
The longest side of the triangle is 21 centimeters long.
Example Question #511 : Geometry
Each of the following answer choices lists the side lengths of a different triangle. Which of these triangles does not have a right angle?


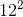

All High School Math Resources






























































