We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : How to find the length of the hypotenuse of a right triangle : Pythagorean Theorem

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #61 : Right Triangles

Righttriangle

Given:

A = 2 miles

B = 3 miles

What is the length of the hypoteneuse of triangle ABC, to the nearest tenth?

Possible Answers:

3.4 miles

3.6 miles

3.2 miles

3.7 miles

3.5 miles

Correct answer:

3.6 miles

Explanation:

Using the Pythagrean Theorem, we know that $a^{2} + b^{2} = c^{2}$ .

This tells us:

$2^{2} + 3^{2} = C^{2}$

$4 + 9 = C^{2}$

$13 = C^{2}$

Taking the square root of both sides, we find that C = 3.6

Report an Error

Example Question #21 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

Given that two sides of a right triangle measure 2 feet and 3 feet, respectively, with a hypoteneuse of x, what is the perimeter of this right triangle (to the nearest tenth)?

Possible Answers:

9.4 feet

18 feet

6.4 feet

3.6 feet

8.6 feet

Correct answer:

8.6 feet

Explanation:

Using the Pythagrean Theorem, we know that $a^{2} + b^{2} = c^{2}$ .

This tells us:

$2^{2} + 3^{2} = C^{2}$

$4 + 9 = C^{2}$

$13 = C^{2}$

Taking the square root of both sides, we find that C = 3.6

To find the perimeter, we add the side lengths together, which gives us that the perimeter is: 3 + 2 + 3.6 = 8.6

Report an Error

Example Question #43 : Right Triangles

$In\;\Delta GHJ, \;what\;is\;the\;length\;of\;\overline{GJ}?$

Possible Answers:

Correct answer:

Explanation:

$Use\;the\;Pythagorean\;Theorem:A^2+B^2=C^2,\;to\; find\;\overline{GJ}.$

5^2+12^2=C^2

25+144=C^2

169=C^2

$C=\sqrt{169}=13$

Report an Error

Example Question #2 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

Kathy and Jill are travelling from their home to the same destination. Kathy travels due east and then after travelling 6 miles turns and travels 8 miles due north. Jill travels directly from her home to the destination. How miles does Jill travel?

Possible Answers:

$\dpi{100} \small 12\ miles$

$\dpi{100} \small 14\ miles$

$\dpi{100} \small 10\ miles$

$\dpi{100} \small 8\ miles$

$\dpi{100} \small 16\ miles$

Correct answer:

$\dpi{100} \small 10\ miles$

Explanation:

Kathy's path traces the outline of a right triangle with legs of 6 and 8. By using the Pythagorean Theorem

$\dpi{100} \small 6^{2}+8^{2}=x^{2}$

$\dpi{100} \small 36+64=x^{2}$

$\dpi{100} \small x=10$ miles

Report an Error

Example Question #51 : Triangles

$Which\; of \;the \;following \;is\; NOT\; true\; about \;the \;hypotenuse \;of \;a\; triangle?$

Possible Answers:

$It\;is\;always\;across\;from\;the\;largest\;angle\;in\;the\;triangle.$

$It\;is\;across\;from\;the\;right\;angle.$

$It\;is\;always\;greater\;than\;1.$

$It\;is\;the\;longest\;side.$

Correct answer:

$It\;is\;always\;greater\;than\;1.$

Explanation:

$The\;hypotenuse\;can\;be\;between\;0\;and\;1.$

Report an Error

Example Question #22 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

In order to get to work, Jeff leaves home and drives 4 miles due north, then 3 miles due east, followed by 6 miles due north and, finally, 7 miles due east. What is the straight line distance from Jeff’s work to his home?

Possible Answers:

2√5

6√2

10√2

Correct answer:

10√2

Explanation:

Jeff drives a total of 10 miles north and 10 miles east. Using the Pythagorean theorem (a²+b²=c²), the direct route from Jeff’s home to his work can be calculated. 10²+10²=c². 200=c². √200=c. √100√2=c. 10√2=c

Report an Error

Example Question #111 : Plane Geometry

Jim leaves his home and walks 10 minutes due west and 5 minutes due south. If Jim could walk a straight line from his current position back to his house, how far, in minutes, is Jim from home?

Possible Answers:

6√6

5√5

√10

√5

Correct answer:

5√5

Explanation:

By using Pythagorean Theorem, we can solve for the distance “as the crow flies” from Jim to his home:

10² + 5² = x²

100 + 25 = x²

√125 = x, but we still need to factor the square root

√125 = √25*5, and since the √25 = 5, we can move that outside of the radical, so

5√5= x

Report an Error

Example Question #61 : Triangles

A square enclosure has a total area of 3,600 square feet. What is the length, in feet, of a diagonal across the field rounded to the nearest whole number?

Possible Answers:

100

Correct answer:

Explanation:

In order to find the length of the diagonal accross a square, we must first find the lengths of the individual sides.

The area of a square is found by multiply the lengths of 2 sides of a square by itself.

So, the square root of 3,600 comes out to 60 ft.

The diagonal of a square can be found by treating it like a right triangle, and so, we can use the pythagorean theorem for a right triangle.

60² + 60² = C²

the square root of 7,200 is 84.8, which can be rounded to 85

Report an Error

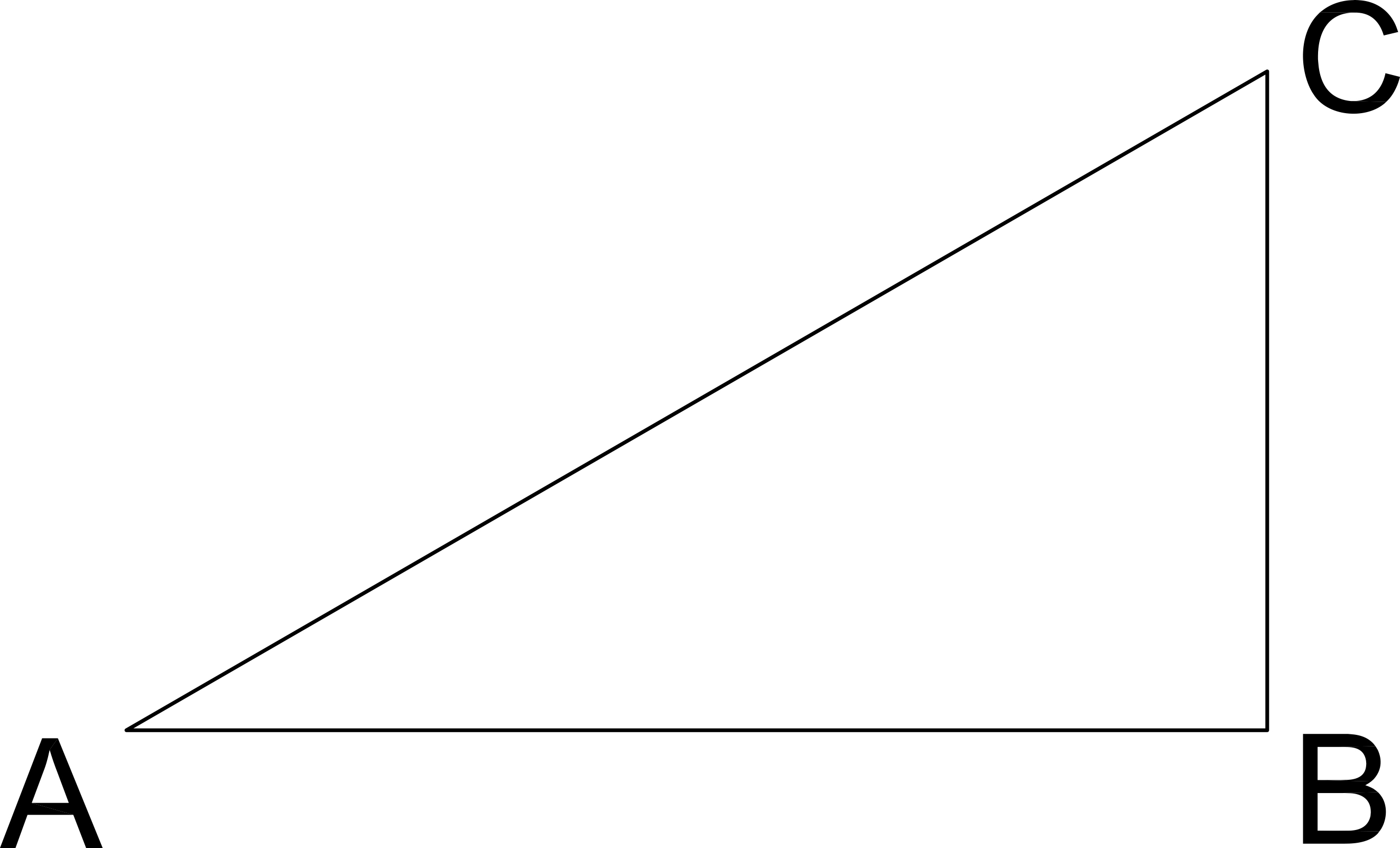
Example Question #52 : Right Triangles

Triangle

If the length of CB is 6 and the angle C measures 45º, what is the length of AC in the given right triangle?

Possible Answers:

12√2

6√2

Correct answer:

6√2

Explanation:

Pythagorean Theorum

AB² + BC² = AC²

If C is 45º then A is 45º, therefore AB = BC

AB² + BC² = AC²

6² + 6² = AC²

2*6² = AC²

AC = √(2*6²) = 6√2

Report an Error

Example Question #71 : Geometry

You leave on a road trip driving due North from Savannah, Georgia, at 8am. You drive for 5 hours at 60mph and then head due East for 2 hours at 50mph. After those 7 hours, how far are you Northeast from Savannah as the crow flies (in miles)?

Possible Answers:

$\sqrt{90000}$

$\sqrt{100000}$

$\sqrt{10000}$

$\sqrt{80000}$

$\sqrt{70000}$

Correct answer:

$\sqrt{100000}$

Explanation:

Distance = hours * mph

North Distance = 5 hours * 60 mph = 300 miles

East Distance = 2 hours * 50 mph = 100 miles

Use Pythagorean Theorem to determine Northeast Distance

300^{2 +}100²=NE²

90000 + 10000 = 100000 = NE²

NE = √100000

Report an Error

View Tutors

Kaylee
Certified Tutor

Brigham Young University, Bachelor, MFA - Animation.

View Tutors

Angela
Certified Tutor

North Georgia College State University, Bachelor of Science, Special Education. North Georgia College State University, Mas...

View Tutors

Dereika
Certified Tutor

Southern University and A & M College, Bachelor of Science, Accounting. Grand Canyon University, Master of Science, Accounting.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Computer Science Tutors in Phoenix, SSAT Tutors in San Diego, LSAT Tutors in Washington DC, Statistics Tutors in New York City, SSAT Tutors in Los Angeles, Computer Science Tutors in Houston, GMAT Tutors in San Diego, Chemistry Tutors in San Diego, English Tutors in Atlanta, SAT Tutors in Philadelphia

Popular Courses & Classes

Spanish Courses & Classes in Philadelphia, GRE Courses & Classes in Washington DC, GRE Courses & Classes in Houston, GMAT Courses & Classes in Miami, ACT Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Miami, GMAT Courses & Classes in Seattle, SAT Courses & Classes in Atlanta, MCAT Courses & Classes in Miami, SSAT Courses & Classes in Seattle

Popular Test Prep

ISEE Test Prep in New York City, SAT Test Prep in Chicago, ISEE Test Prep in Phoenix, GMAT Test Prep in Seattle, ACT Test Prep in Philadelphia, LSAT Test Prep in San Diego, SAT Test Prep in Denver, LSAT Test Prep in Phoenix, ACT Test Prep in San Diego, ACT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : How to find the length of the hypotenuse of a right triangle : Pythagorean Theorem

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #61 : Right Triangles

Example Question #21 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

Example Question #43 : Right Triangles

Example Question #2 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

Example Question #51 : Triangles

Example Question #22 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

Example Question #111 : Plane Geometry

Example Question #61 : Triangles

Example Question #52 : Right Triangles

Example Question #71 : Geometry

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: