We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #3 : How To Find The Volume Of A Rectangular Solid In Pre Algebra

What is the side of a cube if its volume is 125 ?

Possible Answers:

Correct answer:

Explanation:

The formula for volume of a cube is V=s*s*s or V=s^3 .

For this cube that means 125=s^3 .

Take the cube root of both sides:

$\sqrt[3]{125}=\sqrt[3]{s^3}$

5=s

Report an Error

Example Question #4 : How To Find The Volume Of A Rectangular Solid In Pre Algebra

What is the volume of a rectangular prism with a length of , height of , and width of ?

Possible Answers:

216

Correct answer:

Explanation:

The formula for volume of a rectangular prism is V=l*w*h .

Plug in our given information:

V=6*3*4

V=72

Report an Error

Example Question #4 : How To Find The Volume Of A Rectangular Solid In Pre Algebra

What is the volume of a rectangular prism with a length of , width of , and height of ?

Possible Answers:

210

Correct answer:

210

Explanation:

The formula for volume of a rectangular prism is V=l*w*h .

Plug in our given information:

V=7*5*6

V=210

Report an Error

Example Question #5 : How To Find The Volume Of A Rectangular Solid In Pre Algebra

What is the volume of a cube with a side length of ?

Possible Answers:

V=256

V=4096

V=16

V=64

Correct answer:

V=4096

Explanation:

To find the volume of a cube you must cube the side length.

The equation looks like this: $Volume=s^{3}$

Cube the side length, , to find the answer: $V=16^{3}$

The answer is V=4096 .

Report an Error

Example Question #1 : How To Find The Volume Of A Rectangular Solid In Pre Algebra

What is the volume of a rectangular solid with a base of , length of , and height of ?

Possible Answers:

V=756

V=28

V=326

Correct answer:

V=756

Explanation:

To find the volume of a rectangular solid we must know the equation: Volume=b*l*h

We then plug in our numbers for base, length, and height: Volume=7*9*12

Multiply to get the answer of V=756 .

Report an Error

Example Question #2 : How To Find The Volume Of A Rectangular Solid In Pre Algebra

What is the volume of a cube with a side length of ?

Possible Answers:

V=16

V=32

V=64

V=128

Correct answer:

V=64

Explanation:

To find the volume of a cube you must find the cube root of the side length.

The equation looks like this

$V=s^{3}$

Cube the side length, to find the answer

$V=4^{3}$

The answer is V=64 .

Report an Error

Example Question #6 : How To Find The Volume Of A Rectangular Solid In Pre Algebra

What is the volume of a rectangular solid with a base of , length of , and a height of ?

Possible Answers:

V=40

V=400

V=360

V=270

Correct answer:

V=360

Explanation:

To find the volume of a rectangular solid we must know the equation is

V=Base*Height*Length

We then plug in our numbers for base, length, and height

$V=8\cdot 5\cdot 9$

Multiply to get the answer of V=360 .

Report an Error

Example Question #1 : 45/45/90 Right Isosceles Triangles

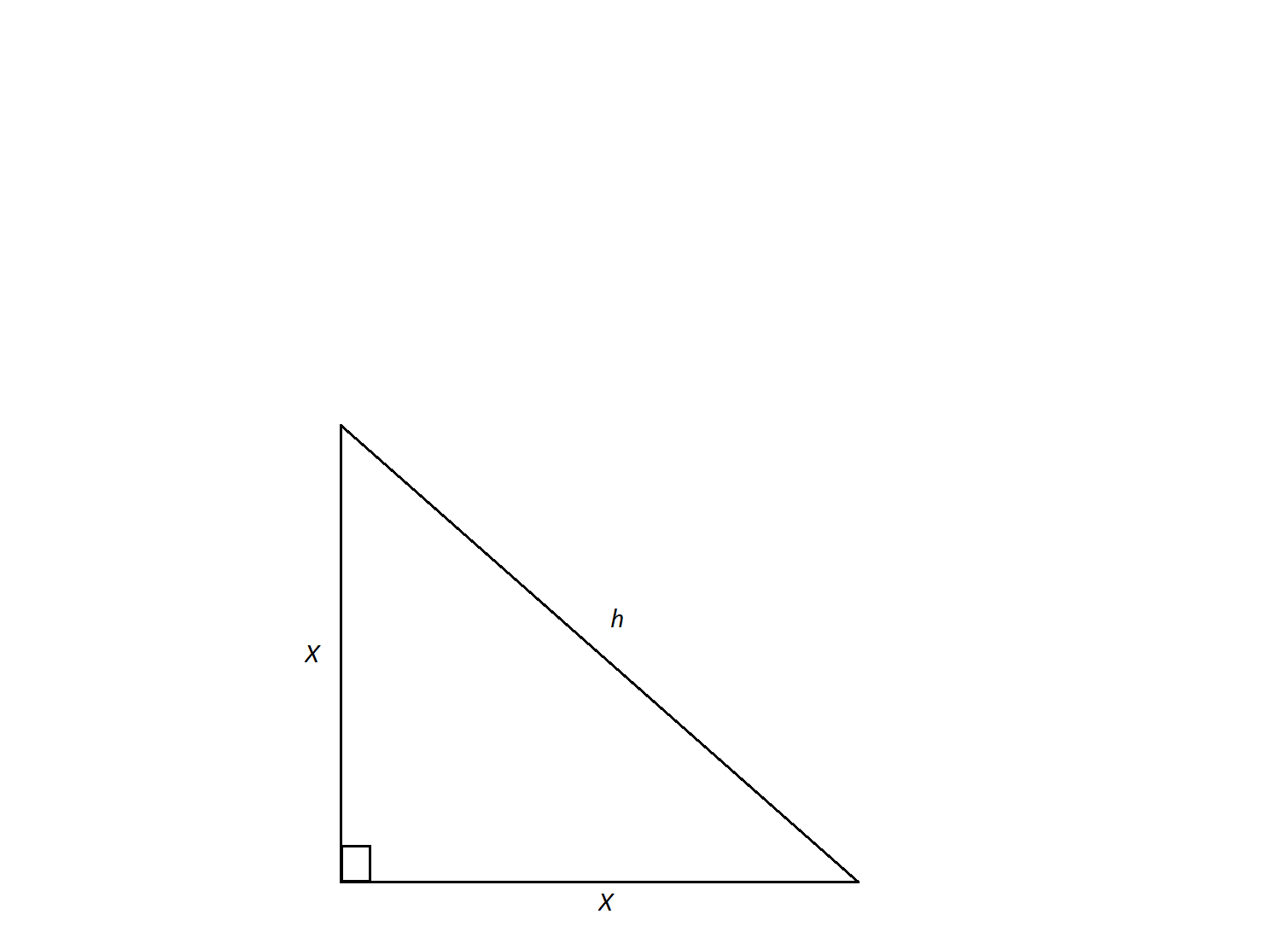
Isosceles

In an isosceles right triangle, two sides equal . Find the length of side .

Possible Answers:

$\sqrt{x}$

$2\sqrt{2}$

$x\sqrt{2}$

$\sqrt{2}$

Correct answer:

$x\sqrt{2}$

Explanation:

This problem represents the definition of the side lengths of an isosceles right triangle. By definition the sides equal , , and $x\sqrt{2}$ . However, if you did not remember this definition one can also find the length of the side using the Pythagorean theorem $(a^{2}+b^{2}=c^{2})$ .

$h^{2}=x^{2}+x^{2}$

$h^{2}=2x^{2}$

$h=\sqrt{2x^{2}}$

$\rightarrow x\sqrt{2}$

Report an Error

Example Question #1 : 45/45/90 Right Isosceles Triangles

ABCD is a square whose side is units. Find the length of diagonal AC.

Possible Answers:

$8\sqrt{3}$

none of the other answers

$8 \sqrt{2}$

Correct answer:

$8 \sqrt{2}$

Explanation:

To find the length of the diagonal, given two sides of the square, we can create two equal triangles from the square. The diagonal line splits the right angles of the square in half, creating two triangles with the angles of , , and degrees. This type of triangle is a special right triangle, with the relationship between the side opposite the degree angles serving as x, and the side opposite the degree angle serving as $x\sqrt{2}$ .

Appyling this, if we plug in for we get that the side opposite the right angle (aka the diagonal) is $8\sqrt{2}$

Report an Error

Example Question #1 : 45/45/90 Right Isosceles Triangles

The area of a square is 144 . Find the length of the diagonal of the square.

Possible Answers:

$4\sqrt{2}$

$16\sqrt{2}$

$12\sqrt{2}$

Correct answer:

$12\sqrt{2}$

Explanation:

If the area of the square is 144 , we know that each side of the square is , because the area of a square is $s^{2}$ .

Then, the diagonal creates two 45/45/90 special right triangles. Knowing that the sides = , we can find that the hypotenuse (aka diagonal) is $12\sqrt{2}$

Report an Error

View Tutors

Michael
Certified Tutor

University of Michigan-Ann Arbor, Bachelor in Arts, History.

View Tutors

Ahmad
Certified Tutor

American University of Beirut, Bachelor of Science, Chemistry. Wayne State University, Doctor of Philosophy, Organic Chemistry.

View Tutors

Monia
Certified Tutor

Institut National des Sciences Appliquees, Bachelor of Science, Computer Science. Concordia University-Ann Arbor, Master of S...

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in Seattle, Biology Tutors in Miami, Chemistry Tutors in Los Angeles, Spanish Tutors in Houston, Physics Tutors in Seattle, English Tutors in Seattle, Calculus Tutors in Boston, ACT Tutors in Denver, ISEE Tutors in Houston, Reading Tutors in Chicago

Popular Courses & Classes

SSAT Courses & Classes in Denver, ACT Courses & Classes in Atlanta, LSAT Courses & Classes in San Diego, ACT Courses & Classes in Philadelphia, Spanish Courses & Classes in Chicago, ACT Courses & Classes in Denver, GMAT Courses & Classes in Miami, SAT Courses & Classes in Chicago, GMAT Courses & Classes in Seattle, GRE Courses & Classes in Houston

Popular Test Prep

ACT Test Prep in Miami, LSAT Test Prep in Atlanta, LSAT Test Prep in Los Angeles, SSAT Test Prep in New York City, SAT Test Prep in Atlanta, MCAT Test Prep in Los Angeles, ACT Test Prep in Denver, GMAT Test Prep in Seattle, ISEE Test Prep in Denver, MCAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #3 : How To Find The Volume Of A Rectangular Solid In Pre Algebra

Example Question #4 : How To Find The Volume Of A Rectangular Solid In Pre Algebra

Example Question #4 : How To Find The Volume Of A Rectangular Solid In Pre Algebra

Example Question #5 : How To Find The Volume Of A Rectangular Solid In Pre Algebra

Example Question #1 : How To Find The Volume Of A Rectangular Solid In Pre Algebra

Example Question #2 : How To Find The Volume Of A Rectangular Solid In Pre Algebra

Example Question #6 : How To Find The Volume Of A Rectangular Solid In Pre Algebra

Example Question #1 : 45/45/90 Right Isosceles Triangles

Example Question #1 : 45/45/90 Right Isosceles Triangles

Example Question #1 : 45/45/90 Right Isosceles Triangles

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: