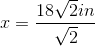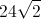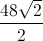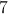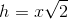We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : 45/45/90 Right Isosceles Triangles

Isosceles

An isosceles right triangle has a hypotenuse of $h=18\sqrt{2} in$ . Find its area.

Possible Answers:

Not enough information to solve

$5.4ft^{2}$

$4.5ft^{2}$

$1.125ft^{2}$

$2.115ft^{2}$

Correct answer:

$1.125ft^{2}$

Explanation:

In order to calculate the triangle's area, we need to find the lengths of its legs. An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as $45^{\circ}-45^{\circ}-90^{\circ}$ triangles and their side lengths follow a specific pattern that states that one can calculate the length of the legs of an isoceles triangle by dividing the length of the hypotenuse by the square root of 2.

$x=\frac{h}{\sqrt{2}}$

$x=\frac{18\sqrt{2}in}{\sqrt{2}}$

x=18in

Now we can calculate the area using the formula

$A=\frac{1}{2}bh$

$A=\frac{1}{2}*18in*18in$

$A=162in^{2}$

Now, convert to feet.

$\rightarrow \frac{162 in^{2}}{1}*\frac{1ft}{12in}*\frac{1ft}{12in}=1.125ft^{2}$

Report an Error

Example Question #2 : 45/45/90 Right Isosceles Triangles

The base of a right isosceles triangle is 8 inches. The hypotenuse is not the base. What is the area of the triangle in inches?

Possible Answers:

128

Correct answer:

Explanation:

To find the area of a triangle, multiply the base by the height, then divide by 2. Since the short legs of an isosceles triangle are the same length, we need to know only one to know the other. Since, a short side serves as the base of the triangle, the other short side tells us the height.

$(8\cdot 8)/2=32$

Report an Error

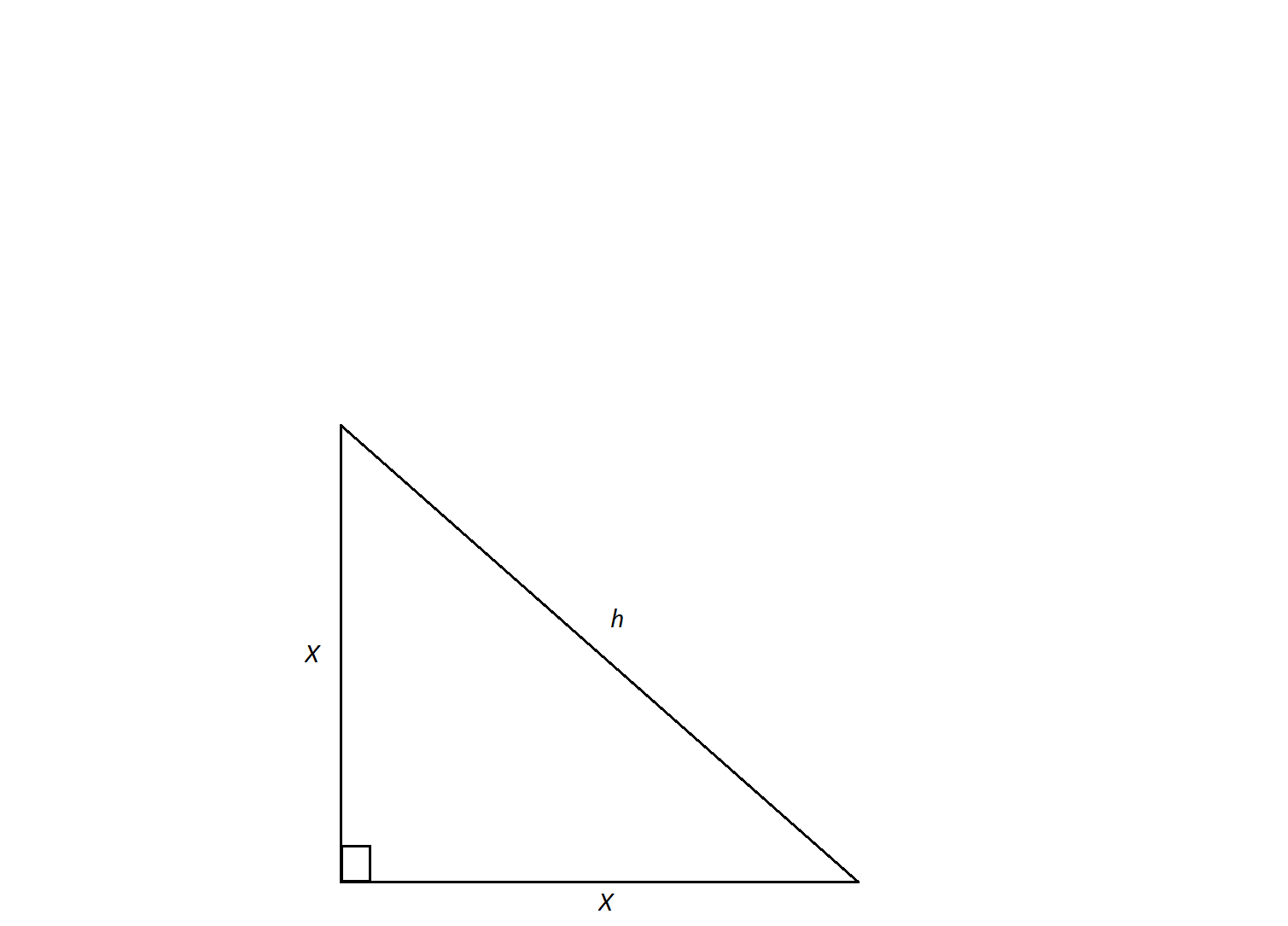
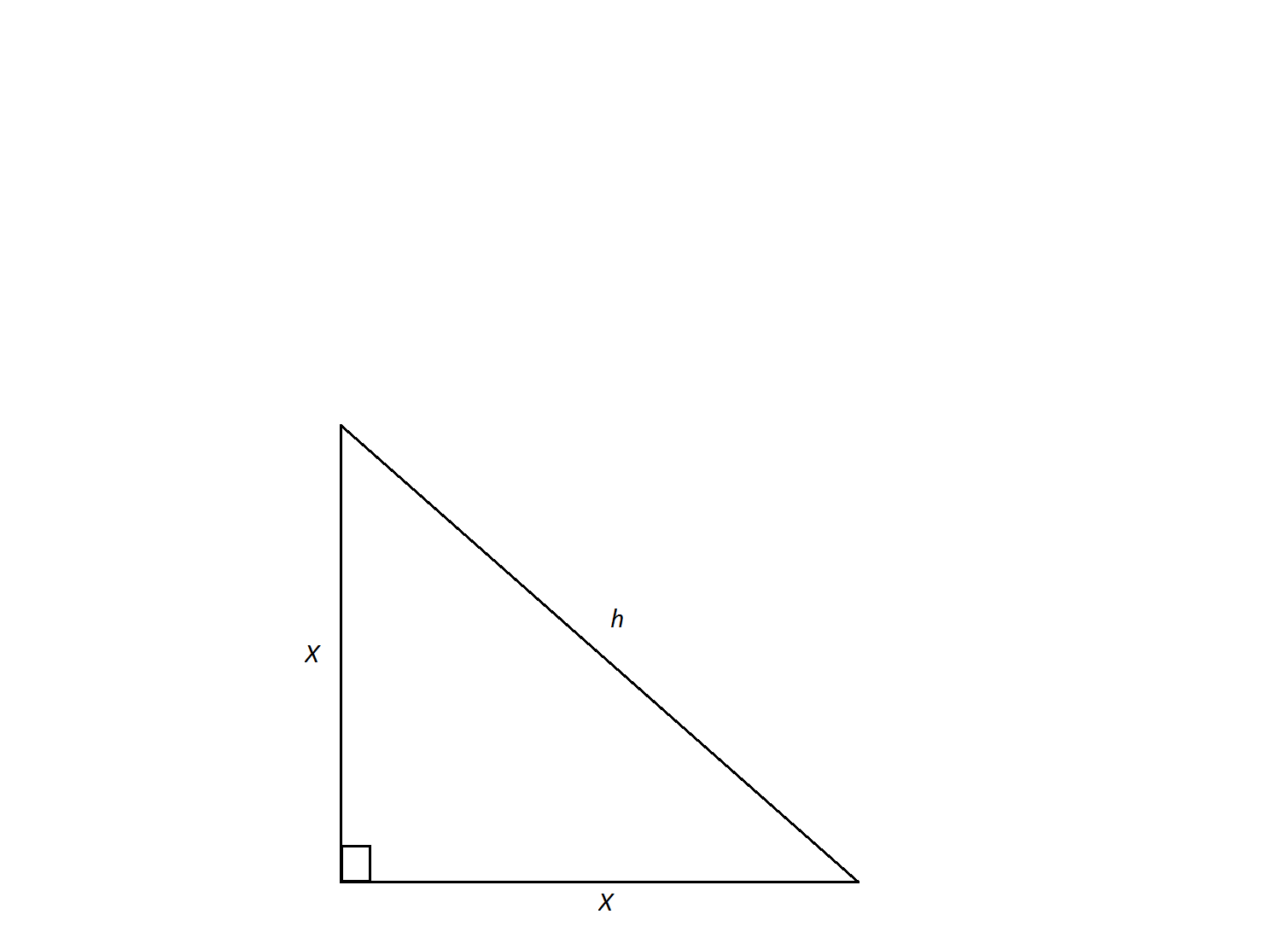
Example Question #4 : 45/45/90 Right Isosceles Triangles

Isosceles

The hypotenuse of an isosceles right triangle has a measure of h=8cm . Find its perimeter.

Possible Answers:

19.31cm

Not enough information to solve

13.92cm

12.32cm

20.22cm

Correct answer:

19.31cm

Explanation:

In order to calculate the triangle's perimeter, we need to find the lengths of its legs. An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as $45^{\circ}-45^{\circ}-90^{\circ}$ triangles and their side lengths follow a specific pattern that states that one can calculate the length of the legs of an isoceles triangle by dividing the length of the hypotenuse by the square root of 2.

$x=\frac{h}{\sqrt{2}}$

$x=\frac{8}{\sqrt{2}}$

$x=4\sqrt{2}$

Now we can calculate the perimeter by doubling and adding .

P=2x+h

$P=(2*4\sqrt{2})+8cm$

P=19.31cm

Report an Error

Example Question #3 : 45/45/90 Right Isosceles Triangles

Isosceles

The side lengths of an isoceles right triangle measure x=14cm . Find its perimeter.

Possible Answers:

42cm

48.70cm

47.80cm

40.87cm

Not enough information to solve

Correct answer:

47.80cm

Explanation:

An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as $45^{\circ}-45^{\circ}-90^{\circ}$ triangles and their side lenghts follow a specific pattern that states you can calculate the length of the hypotenuse of an isoceles triangle by multiplying the length of one of the legs by the square root of 2.

$h=x\sqrt{2}$

$h=14cm\sqrt{2}$

h=19.80cm

Now we can calculate the perimeter by doubling and adding .

P=2x+h

P=(14cm*2)+19.80cm

P=47.8cm

Report an Error

Example Question #2 : 45/45/90 Right Isosceles Triangles

A triangle has two angles equal to $45^\circ$ and two sides equal to . What is the perimeter of this triangle?

Possible Answers:

$\frac{48\sqrt{2}}{2}$

$16+8\sqrt{2}$

$24\sqrt{2}$

Correct answer:

$16+8\sqrt{2}$

Explanation:

When a triangle has two angles equal to $45^\circ$ , it must be a $45^\circ:45^\circ:90^\circ$ isosceles right triangle.

The pattern for the sides of a $45^\circ:45^\circ:90^\circ$ is $x:x:x\sqrt{2}$ .

Since two sides are equal to , this triangle will have sides of $8:8:8\sqrt{2}$ .

Add them all together to get $16+8\sqrt{2}$ .

Report an Error

Example Question #1 : 45/45/90 Right Isosceles Triangles

An isosceles triangle has a base of 6 and a height of 4. What is the perimeter of the triangle?

Possible Answers:

None of these

Correct answer:

Explanation:

An isosceles triangle is basically two right triangles stuck together. The isosceles triangle has a base of 6, which means that from the midpoint of the base to one of the angles, the length is 3. Now, you have a right triangle with a base of 3 and a height of 4. The hypotenuse of this right triangle, which is one of the two congruent sides of the isosceles triangle, is 5 units long (according to the Pythagorean Theorem).

The total perimeter will be the length of the base (6) plus the length of the hypotenuse of each right triangle (5).

5 + 5 + 6 = 16

Report an Error

Example Question #5 : 45/45/90 Right Isosceles Triangles

What is the area of a square that has a diagonal whose endpoints in the coordinate plane are located at (-8, 6) and (2, -4)?

Possible Answers:

100

100√2

200√2

50√2

Correct answer:

100

Explanation:

Square_part1

Square_part2

Square_part3

Report an Error

Example Question #21 : Triangles

Isosceles

An isosceles triangle has a hypotenuse of h=7in . Find the length of its sides, .

Possible Answers:

Not enough information to solve

7in

5.94in

4.95in

2.64in

Correct answer:

4.95in

Explanation:

An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as $45^{\circ}-45^{\circ}-90^{\circ}$ triangles and their side lengths follow a specific pattern that states you can calculate the length of the legs of an isoceles triangle by dividing the length of the hypotenuse by the square root of 2

$x=\frac{h}{\sqrt{2}}$

$x=\frac{7in}{\sqrt{2}}$

$\rightarrow 4.95in$

Report an Error

Example Question #31 : Triangles

Isosceles

The measure of the sides of this isosceles right triangle are $x=3\sqrt{2}$ . Find the measure of its hypotenuse, .

Possible Answers:

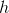
Not enough information to solve

Correct answer:

Explanation:

$h=x\sqrt{2}$

$h=3\sqrt{2}*\sqrt{2}$

h=3*2

$\rightarrow6$

Report an Error

Example Question #1 : How To Find The Volume Of A Cylinder In Pre Algebra

What is the volume of a cylinder with a circular side with a radius of and a length of ?

Possible Answers:

$400\pi$

$72\pi$

$144\pi$

$432\pi$

Correct answer:

$432\pi$

Explanation:

To find the volume of a cylinder we must know the equation for the volume of a cylinder which is

In this example the length is and the radius is so our equation will look like this $Volume=\pi(6^{2})(12)$

We then square the to get .

Then perform multiplication to get $432\pi$ .

The answer is $432\pi$ .

Report an Error

View Tutors

Anthony
Certified Tutor

Purdue University-Main Campus, Bachelor of Science, Computer Engineering, General.

View Tutors

Michael
Certified Tutor

University of Michigan-Ann Arbor, Bachelor in Arts, History.

View Tutors

Ahmad
Certified Tutor

American University of Beirut, Bachelor of Science, Chemistry. Wayne State University, Doctor of Philosophy, Organic Chemistry.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Computer Science Tutors in San Francisco-Bay Area, GMAT Tutors in Boston, LSAT Tutors in Houston, SSAT Tutors in Dallas Fort Worth, Spanish Tutors in Los Angeles, SSAT Tutors in Washington DC, English Tutors in San Francisco-Bay Area, English Tutors in Dallas Fort Worth, LSAT Tutors in Washington DC, MCAT Tutors in New York City

Popular Courses & Classes

SAT Courses & Classes in Houston, GMAT Courses & Classes in Atlanta, GMAT Courses & Classes in San Francisco-Bay Area, SSAT Courses & Classes in Chicago, Spanish Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Washington DC, MCAT Courses & Classes in Chicago, ACT Courses & Classes in Seattle, ISEE Courses & Classes in Chicago

Popular Test Prep

SAT Test Prep in Houston, MCAT Test Prep in Phoenix, SSAT Test Prep in Los Angeles, GRE Test Prep in Philadelphia, ACT Test Prep in New York City, ACT Test Prep in Dallas Fort Worth, ISEE Test Prep in Chicago, GMAT Test Prep in Atlanta, ACT Test Prep in Seattle, LSAT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : 45/45/90 Right Isosceles Triangles

Example Question #2 : 45/45/90 Right Isosceles Triangles

Example Question #4 : 45/45/90 Right Isosceles Triangles

Example Question #3 : 45/45/90 Right Isosceles Triangles

Example Question #2 : 45/45/90 Right Isosceles Triangles

Example Question #1 : 45/45/90 Right Isosceles Triangles

Example Question #5 : 45/45/90 Right Isosceles Triangles

Example Question #21 : Triangles

Example Question #31 : Triangles

Example Question #1 : How To Find The Volume Of A Cylinder In Pre Algebra

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: