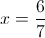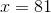All High School Math Resources
Example Questions
Example Question #31 : Polynomials
Factor the following polynomial:
Begin by rearranging the terms to group together the quadratic:
Now, convert the quadratic into a square:
Finally, distribute the 
Example Question #32 : Polynomials
Factor the following polynomial:
Begin by extracting 
Now, rearrange to combine like terms:
Extract the like terms and factor the cubic:
Simplify by combining like terms:
Example Question #33 : Polynomials
Factor the following polynomial:
Begin by extracting 
Now, rearrange to combine like terms:
Extract the like terms and factor the cubic:
Simplify by combining like terms:
Example Question #281 : Algebra Ii
Consider the equation 
According to the Rational Zeroes Theorem, if 
By the Rational Zeroes Theorem, any rational solution must be a factor of the constant, 6, divided by the factor of the leading coefficient, 14.
Four of the answer choices have this characteristic:

Example Question #1 : Understanding Quadratic Equations
Solve the following equation using the quadratic form:
Factor the equation and solve:

or
Therefore there are four answers:
Example Question #2 : Understanding Quadratic Equations
Solve the following equation using the quadratic form:
Factor the equation and solve:

or
This has no solutions.
Therefore there is only one answer:
Example Question #282 : Algebra Ii
Evaluate
In order to evaluate 
Multiply terms by way of FOIL method.
Now multiply and simplify.
Example Question #2 : Using Foil
Evaluate
In order to evaluate 
Multiply terms by way of FOIL method.
Now multiply and simplify, paying attention to signs.
Example Question #1 : Quadratic Equations And Inequalities
Evaluate
In order to evaluate 
Multiply terms by way of FOIL method.
Now multiply and simplify, paying attention to signs.
Example Question #1 : Understanding Quadratic Equations
Evaluate
In order to evaluate 
Multiply terms by way of FOIL method.
Now multiply and simplify, paying attention to signs.
All High School Math Resources

















![mn[(m-n)(m^2+mn+n^2)+1(m-n)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/153204/gif.latex)







![3[(x+1)(x^2-x+1)+3x(x+1)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/153208/gif.latex)
![3[(x+1)(x^2-x+1+3x)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/153209/gif.latex)