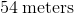High School Math : Geometry
Study concepts, example questions & explanations for High School Math
All High School Math Resources
Example Questions
Example Question #1 : How To Find The Perimeter Of A Rectangle
The length of a rectangle is 3 more inches than its width. The area of the rectangle is 40 in2. What is the perimeter of the rectangle?
34 in.
26 in.
40 in.
18 in.
None of the answers are correct
26 in.
Area of rectangle: A = lw
Perimeter of rectangle: P = 2l + 2w
w = width and l = w + 3
So A = w(w + 3) = 40 therefore w2 + 3w – 40 = 0
Factor the quadratic equation and set each factor to 0 and solve.
w2 + 3w – 40 = (w – 5)(w + 8) = 0 so w = 5 or w = -8.
The only answer that makes sense is 5. You cannot have a negative value for a length.
Therefore, w = 5 and l = 8, so P = 2l + 2w = 2(8) + 2(5) = 26 in.
Example Question #4 : How To Find The Perimeter Of A Rectangle
The length of a rectangle is 
Not enough information to solve
Perimeter of a quadrilateral is found by adding up the lengths of its sides. The formula for the perimeter of a rectangle is 
Example Question #1 : How To Find The Perimeter Of A Rectangle
Kayla took 25 minutes to walk around a rectangular city block. If the block's width is 1/4 the size of the length, how long would it take to walk along one length?
2.5 minutes
7 minutes
8 minutes
10 minutes
10 minutes
Leaving the width to be x, the length is 4x. The total perimeter is 4x + 4x + x + x = 10x.
We divide 25 by 10 to get 2.5, the time required to walk the width. Therefore the time required to walk the length is (4)(2.5) = 10.
Example Question #1 : How To Find The Perimeter Of A Rectangle
Robert is designing a rectangular garden. He wants the area of the garden to be 9 square meters. If the length of the lot is going to be three meters less than twice the width, what will the perimeter of the lot be in meters?
1.5
6
10
12
3
12
Let l be the length of the garden and w be the width.
By the specifications of the problem, l = 2w-3.
Plug this in for length in the area formula:
A = l x w = (2w - 3) x w = 9
Solve for the width:
2w²- 3w - 9 =0
(2w + 3)(w - 3) = 0
w is either 3 or -3/2, but we can't have a negative width, so w = 3.
If w = 3, then length = 2(3) - 3 = 3.
Now plug the width and length into the formula for perimeter:
P = 2 l + 2w = 2(3) + 2(3) = 12
Example Question #1 : How To Find The Perimeter Of A Rectangle
A rectangular garden has an area of 
We define the variables as 
We substitute these values into the equation for the area of a rectangle and get 
Lengths cannot be negative, so the only correct answer is 
Therefore, 
Example Question #1 : Rectangles
The two rectangles shown below are similar. What is the length of EF?
8
6
5
10
10
When two polygons are similar, the lengths of their corresponding sides are proportional to each other. In this diagram, AC and EG are corresponding sides and AB and EF are corresponding sides.
To solve this question, you can therefore write a proportion:
AC/EG = AB/EF ≥ 3/6 = 5/EF
From this proportion, we know that side EF is equal to 10.
Example Question #1 : How To Find The Length Of The Side Of A Rectangle
A rectangle is x inches long and 3x inches wide. If the area of the rectangle is 108, what is the value of x?
3
4
6
12
8
6
Solve for x
Area of a rectangle A = lw = x(3x) = 3x2 = 108
x2 = 36
x = 6
Example Question #1 : How To Find The Length Of The Side Of A Rectangle
If the area of rectangle is 52 meters squared and the perimeter of the same rectangle is 34 meters. What is the length of the larger side of the rectangle if the sides are integers?
14 meters
15 meters
16 meters
12 meters
13 meters
13 meters
Area of a rectangle is = lw
Perimeter = 2(l+w)
We are given 34 = 2(l+w) or 17 = (l+w)
possible combinations of l + w
are 1+16, 2+15, 3+14, 4+13... ect
We are also given the area of the rectangle is 52 meters squared.
Do any of the above combinations when multiplied together= 52 meters squared? yes 4x13 = 52
Therefore the longest side of the rectangle is 13 meters
Example Question #1 : How To Find The Length Of The Side Of A Rectangle
The width, in cm, of a rectangular fence is 2 more than half its length, in cm. Which of the following gives the width, w cm, in terms of length, l cm, of the rectangular fence?
w = ½ l – 2
w = ½ l + 2
w = 2l + 2
w = 2l – 2
w = ½ l + 2
To find the width, we must take half of the length, which means we must divide the length by 2. Then we must take 2 more than that number, which means we must add 2 to the number. Combining these, we get:
w = ½ l + 2
Example Question #2 : How To Find The Length Of The Side Of A Rectangle
The width of a rectangle is 2 inches longer than 3 times its length. Which of the following equations gives the width, w, of the rectangle in terms of its length, l,?
w = 6l +2
w = 3l – 2
w = 1/3l +2
w = 3l + 2
w = 3l + 2
The width equals 3 times the length, so 3l, plus an additional two inches, so + 2, = 3l + 2
All High School Math Resources
