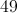High School Math : Plane Geometry
Study concepts, example questions & explanations for High School Math
All High School Math Resources
Example Questions
Example Question #2 : How To Find The Length Of The Side Of A Pentagon
Find the length of the side of the following pentagon.
The perimeter of the pentagon is 
The formula for the perimeter of a regular pentagon is
where 
Plugging in our values, we get:
Example Question #3 : How To Find The Length Of The Side Of A Pentagon
Find the length of the side of the following pentagon.
The perimeter of the pentagon is 
The formula for the perimeter of a regular pentagon is
where
Plugging in our values, we get:
Example Question #1 : How To Find The Area Of A Pentagon
What is the area of a regular pentagon with side length 
The area of a regular polygon can be solved using the following equation: 
To find the perimeterof the pentagon, we multiply the side length by five.
The apothem of a regular polygon (
Pluggin in our numbers, we can solve for the apothem.
Finally, we can solve for the area.
Example Question #1 : How To Find The Area Of A Pentagon
Find the area of the following pentagon:
The formula for the area of of a pentagon is
Plugging in our values, we get:
Example Question #1 : How To Find The Area Of A Pentagon
Find the area of the following pentagon:
The formula for the area of of a pentagon is:
Plugging in our values, we get:
Example Question #1 : Lines
Lines 
When two lines are parallel, corresponding angles are congruent. Because we don't know if lines 
With the given information, we can ignore line 
Example Question #1 : Geometry
Figure not drawn to scale.
In the figure above, APB forms a straight line. If the measure of angle APC is eighty-one degrees larger than the measure of angle DPB, and the measures of angles CPD and DPB are equal, then what is the measure, in degrees, of angle CPB?
66
50
33
114
40
66
Let x equal the measure of angle DPB. Because the measure of angle APC is eighty-one degrees larger than the measure of DPB, we can represent this angle's measure as x + 81. Also, because the measure of angle CPD is equal to the measure of angle DPB, we can represent the measure of CPD as x.
Since APB is a straight line, the sum of the measures of angles DPB, APC, and CPD must all equal 180; therefore, we can write the following equation to find x:
x + (x + 81) + x = 180
Simplify by collecting the x terms.
3x + 81 = 180
Subtract 81 from both sides.
3x = 99
Divide by 3.
x = 33.
This means that the measures of angles DPB and CPD are both equal to 33 degrees. The original question asks us to find the measure of angle CPB, which is equal to the sum of the measures of angles DPB and CPD.
measure of CPB = 33 + 33 = 66.
The answer is 66.
Example Question #1 : Plane Geometry
One-half of the measure of the supplement of angle ABC is equal to the twice the measure of angle ABC. What is the measure, in degrees, of the complement of angle ABC?
54
90
72
36
18
54
Let x equal the measure of angle ABC, let y equal the measure of the supplement of angle ABC, and let z equal the measure of the complement of angle ABC.
Because x and y are supplements, the sum of their measures must equal 180. In other words, x + y = 180.
We are told that one-half of the measure of the supplement is equal to twice the measure of ABC. We could write this equation as follows:
(1/2)y = 2x.
Because x + y = 180, we can solve for y in terms of x by subtracting x from both sides. In other words, y = 180 – x. Next, we can substitute this value into the equation (1/2)y = 2x and then solve for x.
(1/2)(180-x) = 2x.
Multiply both sides by 2 to get rid of the fraction.
(180 – x) = 4x.
Add x to both sides.
180 = 5x.
Divide both sides by 5.
x = 36.
The measure of angle ABC is 36 degrees. However, the original question asks us to find the measure of the complement of ABC, which we denoted previously as z. Because the sum of the measure of an angle and the measure of its complement equals 90, we can write the following equation:
x + z = 90.
Now, we can substitute 36 as the value of x and then solve for z.
36 + z = 90.
Subtract 36 from both sides.
z = 54.
The answer is 54.
Example Question #1 : How To Find The Angle Of Two Lines
In the diagram, AB || CD. What is the value of a+b?
140°
160°
80°
60°
None of the other answers.
160°
Refer to the following diagram while reading the explanation:
We know that angle b has to be equal to its vertical angle (the angle directly "across" the intersection). Therefore, it is 20°.
Furthermore, given the properties of parallel lines, we know that the supplementary angle to a must be 40°. Based on the rule for supplements, we know that a + 40° = 180°. Solving for a, we get a = 140°.
Therefore, a + b = 140° + 20° = 160°
Example Question #2 : How To Find The Angle Of Two Lines
In rectangle ABCD, both diagonals are drawn and intersect at point E.
Let the measure of angle AEB equal x degrees.
Let the measure of angle BEC equal y degrees.
Let the measure of angle CED equal z degrees.
Find the measure of angle AED in terms of x, y, and/or z.
180 – 2(x + z)
180 – (x + y + z)
180 – 1/2(x + z)
180 – y
360 – x + y + z
180 – 1/2(x + z)
Intersecting lines create two pairs of vertical angles which are congruent. Therefore, we can deduce that y = measure of angle AED.
Furthermore, intersecting lines create adjacent angles that are supplementary (sum to 180 degrees). Therefore, we can deduce that x + y + z + (measure of angle AED) = 360.
Substituting the first equation into the second equation, we get
x + (measure of angle AED) + z + (measure of angle AED) = 360
2(measure of angle AED) + x + z = 360
2(measure of angle AED) = 360 – (x + z)
Divide by two and get:
measure of angle AED = 180 – 1/2(x + z)
All High School Math Resources
