Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Plane Geometry

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #481 : Geometry

Equilateral_triangle

An equilateral triangle has a side length of s=4 cm . What is its height, ?

Possible Answers:

3.46cm

5.19cm

1.73cm

Not enough information to solve

4.36cm

Correct answer:

3.46cm

Explanation:

An altitude slices an equilateral triangle into two $30^{\circ}-60^{\circ}-90^{\circ}$ triangles. These triangles follow a side-length pattern. The smallest of the two legs equals and the hypotenuse equals . By way of the Pythagorean Theorem, the longest leg or $h=x\sqrt{3}$ .

Therefore, we can find the height of the altitude of this triangle by designating a value to . The hypotenuse of one of the $30^{\circ}-60^{\circ}-90^{\circ}$ is also the side of the original equilateral triangle. Therefore, one can say that 2x=s=4cm and x=2cm .

$h=x\sqrt{3}$

$h=2\sqrt{3}cm$

$\rightarrow3.46cm$

Report an Error

Example Question #1 : How To Find The Height Of An Equilateral Triangle

What is the height of an equilateral triangle with side 6?

Possible Answers:

$3\sqrt{3}$

$6\sqrt{2}$

Correct answer:

$3\sqrt{3}$

Explanation:

When you draw the height in an equilateral triangle, it makes two 30-60-90 triangles. Because of that relationship, the height (which is across from the $60^{\circ}$ ) is $3\sqrt{3}$ .

Report an Error

Example Question #483 : Plane Geometry

Find the height of the following equilateral triangle:

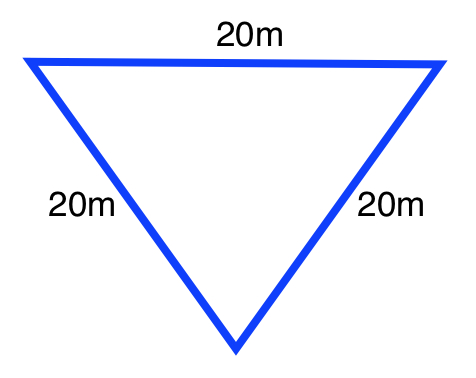
Triangle

Possible Answers:

20m

$20\sqrt{3}m$

10m

$10\sqrt{3}m$

$15\sqrt{3}m$

Correct answer:

$10\sqrt{3}m$

Explanation:

Each angle in an equilateral triangle is $60^{\circ}$ .

Use the formula for 30-60-90 triangles in order to find the length of the height.

The formula is:

$a-a\sqrt{3}-2a$

Where is the length of the side opposite the $\measuredangle 30$

If we were to create a 30-60-90 triangle by drawing the height, the length of the side is 20m , the base is 10m , and the height is $10\sqrt{3}m$ .

Report an Error

Example Question #4 : How To Find The Height Of An Equilateral Triangle

Solve for the value of X in the following equilateral triangle:

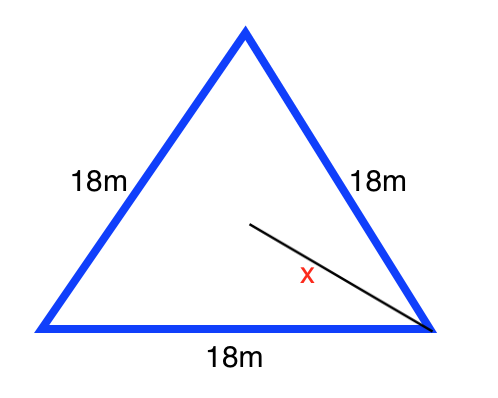
Screen_shot_2014-02-27_at_6.35.43_pm

Possible Answers:

$6\sqrt{3}m$

$3\sqrt{3}m$

$9\sqrt{3}m$

Correct answer:

$6\sqrt{3}m$

Explanation:

If we draw a line segment between X and the base of the triangle, we form a 30-60-90 triangle.

We can use the relationships between the sides of a 30-60-90 triangle in order to find the length of X.

We know the base opposite the $\measuredangle60$ is .

The value of the height opposite the $\measuredangle30$ must then be $\frac{9m\sqrt{3}}{3}$ , or $3\sqrt{3}m$ .

Therefore, the value of X will be twice the value of the height:

$X = 2(3\sqrt{3}m)=6\sqrt{3}m$

Report an Error

Example Question #1 : How To Find The Height Of An Equilateral Triangle

What is the height of an equilateral triangle with a side length of 8 in?

Possible Answers:

$6\sqrt{3}$

$4\sqrt{3}$

$4\sqrt{2}$

$6\sqrt{2}$

Correct answer:

$4\sqrt{3}$

Explanation:

An equilateral triangle has three congruent sides, and is also an equiangular triangle with three congruent angles that each meansure 60 degrees.

To find the height we divide the triangle into two special 30 - 60 - 90 right triangles by drawing a line from one corner to the center of the opposite side. This segment will be the height, and will be opposite from one of the 60 degree angles and adjacent to a 30 degree angle. The special right triangle gives side ratios of , $x\sqrt{3}$ , and . The hypoteneuse, the side opposite the 90 degree angle, is the full length of one side of the triangle and is equal to . Using this information, we can find the lengths of each side fo the special triangle.

$8=2x\rightarrow 4=x\rightarrow 4\sqrt{3}=x\sqrt{3}$

The side with length $x\sqrt{3}$ will be the height (opposite the 60 degree angle). The height is $4\sqrt{3}$ inches.

Report an Error

Example Question #1 : How To Find The Perimeter Of An Equilateral Triangle

Gre11

A square rug border consists of a continuous pattern of equilateral triangles, with isosceles triangles as corners, one of which is shown above. If the length of each equilateral triangle side is 5 inches, and there are 40 triangles in total, what is the total perimeter of the rug?

The inner angles of the corner triangles is 30°.

Possible Answers:

124

188

208

180

200

Correct answer:

188

Explanation:

There are 2 components to this problem. The first, and easier one, is recognizing how much of the perimeter the equilateral triangles take up—since there are 40 triangles in total, there must be 40 – 4 = 36 of these triangles. By observation, each contributes only 1 side to the overall perimeter, thus we can simply multiply 36(5) = 180" contribution.

The second component is the corner triangles—recognizing that the congruent sides are adjacent to the 5-inch equilateral triangles, and the congruent angles can be found by

180 = 30+2x → x = 75°

We can use ratios to find the unknown side:

75/5 = 30/y → 75y = 150 → y = 2''.

Since there are 4 corners to the square rug, 2(4) = 8'' contribution to the total perimeter. Adding the 2 components, we get 180+8 = 188 inch perimeter.

Report an Error

Example Question #2 : How To Find The Perimeter Of An Equilateral Triangle

The height of an equilateral triangle is $\dpi{100} \small 2\sqrt{3}$

What is the triangle's perimeter?

Possible Answers:

$\dpi{100} \small 2\sqrt{2}$

Correct answer:

Explanation:

An altitude drawn in an equilateral triangle will form two 30-60-90 triangles. The height of equilateral triangle is the length of the longer leg of the 30-60-90 triangle. The length of the equilateral triangle's side is the length of the hypotenuse of the 30-60-90.

The ratio of the length of the hypotenuse to the length of the longer leg of a 30-60-90 triangle is $\dpi{100} \small 2:\sqrt{3}$

The length of the longer leg of the 30-60-90 triangle in this problem is $\dpi{100} \small 2\sqrt{3}$

Using this ratio, we find that the length of this triangle's hypotenuse is 4. Thus the perimeter of the equilateral triangle will be 4 multiplied by 3, which is 12.

Report an Error

Example Question #21 : Equilateral Triangles

Equilateral_triangle

An equilateral triangle has a side length of $s=\sqrt{3}$ . What is its perimeter?

Possible Answers:

Not enough information to solve.

3.46

2.50

5.20

6.43

Correct answer:

5.20

Explanation:

An equilateral triangle possesses three sides of equal lengths. Therefore, we can easily calculate its perimeter by tripling the given side length.

P=3*s

$P=3*\sqrt{3}$

$\rightarrow 5.20$

Report an Error

Example Question #22 : Equilateral Triangles

Equilateral_triangle

An equilateral triangle has an altitude length of $h=2\sqrt{3}$ . What is its perimeter?

Possible Answers:

10.39

13.09

Not enough information to solve

Correct answer:

Explanation:

An altitude slices an equilateral triangle into two $30^{\circ}-60^{\circ}-90^{\circ}$ triangles. These triangles follow a side length pattern. The smallest of the two legs equals and the hypotenuse equals . By way of the Pythagorean Theorem, the longest leg or $h=x\sqrt{3}$ .

We have the length of the altitude of the triangle $h=\sqrt{3}$ . We can solve for the smallest side via substitution and simple algebra.

$h=x\sqrt{3}$

$2\sqrt{3}=x\sqrt{3}$

$x=\frac{2\sqrt{3}}{\sqrt{3}}$

x=2

Note, this is only the smallest side of one of the $30^{\circ}-60^{\circ}-90^{\circ}$ triangles. It needs to be doubled to equal a complete side of the equilateral triangle.

s=2x

s=4

Now, the side length can be tripled to calculate the perimeter.

P=3s

P=3*4

$\rightarrow12$

Report an Error

Example Question #1 : How To Find The Perimeter Of An Equilateral Triangle

Find the perimeter of the following equilateral triangle:

Triangle

Possible Answers:

40m

20m

60m

120m

80m

Correct answer:

60m

Explanation:

The formula for the perimeter of an equilateral triangle is:

P=3(s)

Where is the length of the side

Plugging in our values, we get:

P=3(20m)=60m

Report an Error

View Tutors

Joanna
Certified Tutor

Texas Christian University, Bachelor of Education, English.

View Tutors

Abhisek
Certified Tutor

University of Florida, Bachelor of Engineering, Computer Science.

View Tutors

Myrtle
Certified Tutor

Southern University and A M College, Bachelor of Education, English. New Mexico State University-Main Campus, Doctor of Educ...

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Miami, Calculus Tutors in San Francisco-Bay Area, ACT Tutors in Washington DC, ACT Tutors in Houston, SSAT Tutors in New York City, Physics Tutors in Phoenix, Spanish Tutors in Washington DC, Math Tutors in Seattle, Statistics Tutors in Atlanta, LSAT Tutors in Atlanta

Popular Courses & Classes

GRE Courses & Classes in Dallas Fort Worth, Spanish Courses & Classes in Chicago, SSAT Courses & Classes in Los Angeles, GRE Courses & Classes in Boston, ISEE Courses & Classes in Washington DC, LSAT Courses & Classes in Miami, MCAT Courses & Classes in Miami, MCAT Courses & Classes in Phoenix, ACT Courses & Classes in Washington DC, ACT Courses & Classes in Miami

Popular Test Prep

ISEE Test Prep in Los Angeles, GMAT Test Prep in Boston, SSAT Test Prep in Seattle, ISEE Test Prep in Washington DC, ACT Test Prep in Houston, SSAT Test Prep in Houston, LSAT Test Prep in Los Angeles, LSAT Test Prep in New York City, GMAT Test Prep in San Francisco-Bay Area, ACT Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Plane Geometry

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #481 : Geometry

Example Question #1 : How To Find The Height Of An Equilateral Triangle

Example Question #483 : Plane Geometry

Example Question #4 : How To Find The Height Of An Equilateral Triangle

Example Question #1 : How To Find The Height Of An Equilateral Triangle

Example Question #1 : How To Find The Perimeter Of An Equilateral Triangle

Example Question #2 : How To Find The Perimeter Of An Equilateral Triangle

Example Question #21 : Equilateral Triangles

Example Question #22 : Equilateral Triangles

Example Question #1 : How To Find The Perimeter Of An Equilateral Triangle

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: