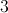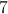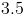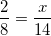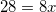All High School Math Resources
Example Questions
Example Question #1 : How To Find The Angle Of Clock Hands
What is the measure of the smaller angle formed by the hands of an analog watch if the hour hand is on the 10 and the minute hand is on the 2?
120°
90°
56°
30°
45°
120°
A analog clock is divided up into 12 sectors, based on the numbers 1–12. One sector represents 30 degrees (360/12 = 30). If the hour hand is directly on the 10, and the minute hand is on the 2, that means there are 4 sectors of 30 degrees between then, thus they are 120 degrees apart (30 * 4 = 120).
Example Question #3 : How To Find The Angle Of Clock Hands
What is the measure, in degrees, of the acute angle formed by the hands of a 12-hour clock that reads exactly 3:10?
60°
65°
55°
72°
35°
35°
The entire clock measures 360°. As the clock is divided into 12 sections, the distance between each number is equivalent to 30° (360/12). The distance between the 2 and the 3 on the clock is 30°. One has to account, however, for the 10 minutes that have passed. 10 minutes is 1/6 of an hour so the hour hand has also moved 1/6 of the distance between the 3 and the 4, which adds 5° (1/6 of 30°). The total measure of the angle, therefore, is 35°.
Example Question #1 : How To Find The Area Of A Kite
What is the area of a kite with diagonals of 5 and 7?
To find the area of a kite using diagonals you use the following equation 
That diagonals (

Plug in the diagonals for 

Then multiply and divide to get the area.
The answer is
Example Question #2 : How To Find The Area Of A Kite
Find the area of the following kite:

The formula for the area of a kite is:
Where 

Plugging in our values, we get:
Example Question #3 : How To Find The Area Of A Kite
Find the area of the following kite:

The formula for the area of a kite is:
where 

Use the formulas for a 





Our 
Our 
Plugging in our values, we get:
Example Question #1 : Kites
Find the perimeter of the following kite:

In order to find the length of the two shorter edges, use a Pythagorean triple:
In order to find the length of the two longer edges, use the Pythagorean theorem:
The formula of the perimeter of a kite is:
Plugging in our values, we get:
Example Question #4 : Quadrilaterals
Find the perimeter of the following kite:

The formula for the perimeter of a kite is:
Where 

Use the formulas for a 





Our 
Our 
Plugging in our values, we get:
Example Question #1 : Trapezoids
When polygons are similar, the sides will have the same ratio to one another. Set up the appropriate proportions.
Cross multiply.
Example Question #6 : Quadrilaterals
Find the area of the following trapezoid:

The formula for the area of a trapezoid is:
Where 


To find the height of the trapezoid, use a Pythagorean triple:
Plugging in our values, we get:
Example Question #7 : Quadrilaterals
Find the area of the following trapezoid:

Use the formula for 
The formula is:
Where 

Beginning with the 



Creating another 



The formula for the area of a trapezoid is:
Where 


Plugging in our values, we get:
All High School Math Resources


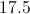













































 .
.