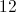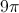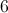Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Plane Geometry

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #31 : Circles

Consider a circle centered at the origin with a circumference of $13\pi$ . What is the x value when y = 3? Round your answer to the hundreths place.

Possible Answers:

5.77

10.00

5.8

None of the available answers

5.778

Correct answer:

5.77

Explanation:

The formula for circumference of a circle is $C=2\pi r$ , so we can solve for r:

$2\pi r=13\pi$

$\frac{2\pi r}{\pi}=\frac{13\pi}{\pi}$

$2r=13$

$r=\frac{13}{2}=6.5$

We now know that the hypotenuse of the right triangle's length is 13.5. We can form a right triangle from the unit circle that fits the Pythagorean theorem as such:

$x^2+y^2=r^2$

Or, in this case:

$x^2+3^3=6.5^2$

$x^2=42.26-9$

$x^2=33.25$

$x=\sqrt{33.25}=5.77$

Report an Error

Example Question #1 : How To Find The Length Of A Radius

What is the radius of a circle with a circumference of $20\pi$ ?

Possible Answers:

$10\pi$

$20\pi$

Correct answer:

Explanation:

To find the radius of a circle given the circumference we must first know the equation for the circumference of a circle which is

Then we plug in the circumference into the equation yielding

$20\pi=2r\pi$

We then divide each side by $2\pi$ giving us 10=r

The answer is r=10 .

Report an Error

Example Question #1 : How To Find The Length Of A Radius

A circle has an area of 36π inches. What is the radius of the circle, in inches?

Possible Answers:

Correct answer:

Explanation:

We know that the formula for the area of a circle is πr². Therefore, we must set 36π equal to this formula to solve for the radius of the circle.

36π = πr²

36 = r²

6 = r

Report an Error

Example Question #1 : How To Find The Length Of A Radius

Circle X is divided into 3 sections: A, B, and C. The 3 sections are equal in area. If the area of section C is 12π, what is the radius of the circle?

Act_math_170_02

Circle X

Possible Answers:

√12

Correct answer:

Explanation:

Find the total area of the circle, then use the area formula to find the radius.

Area of section A = section B = section C

Area of circle X = A + B + C = 12π+ 12π + 12π = 36π

Area of circle = where r is the radius of the circle

36π = πr²

36 = r²

√36 = r

6 = r

Report an Error

Example Question #2 : How To Find The Length Of A Radius

The specifications of an official NBA basketball are that it must be 29.5 inches in circumference and weigh 22 ounces. What is the approximate radius of the basketball?

Possible Answers:

9.39 inches

4.70 inches

3.06 inches

5.43 inches

14.75 inches

Correct answer:

4.70 inches

Explanation:

To Find your answer, we would use the formula: C=2πr. We are given that C = 29.5. Thus we can plug in to get [29.5]=2πr and then multiply 2π to get 29.5=(6.28)r. Lastly, we divide both sides by 6.28 to get 4.70=r. (The information given of 22 ounces is useless)

Report an Error

Example Question #2 : How To Find The Length Of A Radius

If the circumference of a circle is $36\pi$ , what is the radius?

Possible Answers:

$9\pi$

Correct answer:

Explanation:

The formula for circumference is $C=2\pi r$ .

Plug in our given information.

$C=2\pi r$

$36\pi=2\pi r$

Divide both sides by $2\pi$ .

$\frac{36\pi}{2\pi}=\frac{2\pi}{2\pi} r$

18=r

Report an Error

Example Question #1 : How To Find The Length Of A Radius

Find the radius of a circle with area $169\pi$ .

Possible Answers:

169

13.5

Correct answer:

Explanation:

Since the formula for the area of a triangle is

$A=\pi r^2$

plug in the given area and isolate for . This yields 13.

Report an Error

Example Question #111 : Plane Geometry

The circumference of a circle is 45 inches. The circle's radius is ____ inches.

Possible Answers:

14.33

22.5

3.14

7.16

Correct answer:

7.16

Explanation:

When you know the circumference of a circle, you can determine its diameter by dividing the circumference by $\pi$ . Then, when you have the diameter, you can determine the radius by dividing the diameter by 2.

Report an Error

Example Question #3 : How To Find The Length Of A Radius

A circle with center (8, –5) is tangent to the y-axis in the standard (x,y) coordinate plane. What is the radius of this circle?

Possible Answers:

Correct answer:

Explanation:

For the circle to be tangent to the y-axis, it must have its outer edge on the axis. The center is 8 units from the edge.

Report an Error

Example Question #3 : How To Find The Length Of A Radius

A circle has an area of $49\pi \ in^{2}$ . What is the radius of the circle, in inches?

Possible Answers:

14 inches

49 inches

24.5 inches

16 inches

7 inches

Correct answer:

7 inches

Explanation:

We know that the formula for the area of a circle is πr². Therefore, we must set 49π equal to this formula to solve for the radius of the circle.

49π = πr²

49 = r²

7 = r

Report an Error

View Tutors

Brandon
Certified Tutor

University of Houston, Bachelor of Science, Biology, General. University of North Texas, Doctor of Philosophy, Pharmacy.

View Tutors

Linda
Certified Tutor

Pomona College, Bachelor of Science, Political Science and Government.

View Tutors

Paige
Certified Tutor

Chicago State University, Bachelor in Arts, Psychology.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in New York City, LSAT Tutors in San Diego, French Tutors in Denver, GMAT Tutors in Dallas Fort Worth, GRE Tutors in San Francisco-Bay Area, Chemistry Tutors in Seattle, Statistics Tutors in Houston, Reading Tutors in Philadelphia, Calculus Tutors in New York City, ACT Tutors in Boston

Popular Courses & Classes

ISEE Courses & Classes in Los Angeles, SAT Courses & Classes in New York City, ACT Courses & Classes in Houston, ACT Courses & Classes in Seattle, GRE Courses & Classes in Los Angeles, MCAT Courses & Classes in Washington DC, SSAT Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Miami, GRE Courses & Classes in Washington DC, ACT Courses & Classes in Boston

Popular Test Prep

MCAT Test Prep in Washington DC, SSAT Test Prep in Atlanta, SSAT Test Prep in Houston, ACT Test Prep in Denver, LSAT Test Prep in Chicago, SAT Test Prep in Washington DC, SSAT Test Prep in Dallas Fort Worth, ACT Test Prep in Houston, ACT Test Prep in Boston, ACT Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Plane Geometry

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #31 : Circles

Example Question #1 : How To Find The Length Of A Radius

Example Question #1 : How To Find The Length Of A Radius

Example Question #1 : How To Find The Length Of A Radius

Example Question #2 : How To Find The Length Of A Radius

Example Question #2 : How To Find The Length Of A Radius

Example Question #1 : How To Find The Length Of A Radius

Example Question #111 : Plane Geometry

Example Question #3 : How To Find The Length Of A Radius

Example Question #3 : How To Find The Length Of A Radius

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: