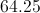Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Calculus II — Integrals

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #15 : Finding Integrals

$\int^5_25x+8{\mathrm{d} x}$ ?

Possible Answers:

102.5

76.5

128.5

64.25

Correct answer:

76.5

Explanation:

Remember the fundamental theorem of calculus! If g'(x)=f(x) , then $\int^b_af(x){\mathrm{d} x}=g(b)-g(a)$ .

Since we're given f(x) , we need to find the indefinite integral of the equation to get g(x) .

To solve for the indefinite integral, we can use the reverse power rule. We raise the power of the exponents by one and divide by that new exponent. For this problem, that would look like:

$\int 5x+8{\mathrm{d} x}=\frac{5x^{1+1}}{1+1}+\frac{8x^{0+1}}{0+1}+c$

Remember, when taking an integral, definite or indefinite, we always add , as there could be a constant involved.

$\int 5x+8{\mathrm{d} x}=\frac{5x^{2}}{2}+\frac{8x^{1}}{1}+c$

$\int 5x+8{\mathrm{d} x}=\frac{5}{2}x^2+8x +c$

Now we can plug that back in:

$\int^b_a 5x+8{\mathrm{d} x}=(\frac{5}{2}b^2+8b +c)-(\frac{5}{2}a^2+8a +c)$

Notice that the 's cancel out.

Plug in our given numbers.

$\int^5_2 5x+8{\mathrm{d} x}=(\frac{5}{2}(5)^2+8*5)-(\frac{5}{2}(2)^2+8*2)$

$\int^5_2 5x+8{\mathrm{d} x}=(\frac{5}{2}*25+40)-(\frac{5}{2}*4+16)$

$\int^5_2 5x+8{\mathrm{d} x}=(62.5+40)-(10+16)$

$\int^5_2 5x+8{\mathrm{d} x}=(102.5)-(26)$

$\int^5_2 5x+8{\mathrm{d} x}=76.5$

Report an Error

Example Question #91 : Asymptotic And Unbounded Behavior

$\int_4^5 x^3+2x+5$ ?

Possible Answers:

106.25

53.5

100

206.25

306.25

Correct answer:

106.25

Explanation:

Remember the fundamental theorem of calculus! If g'(x)=f(x) , then $\int^b_af(x){\mathrm{d} x}=g(b)-g(a)$ .

Since we're given f(x) , we need to find the indefinite integral of the equation to get g(x) .

To solve for the indefinite integral, we can use the reverse power rule. We raise the power of the exponents by one and divide by that new exponent.

We're going to treat as 5x^0 , as anything to the zero power is one.

For this problem, that would look like:

$\int x^3+2x+5{\mathrm{d} x}=\frac{x^{3+1}}{3+1}+\frac{2x^{1+1}}{1+1}+\frac{5x^{0+1}}{0+1}+c$

Remember, when taking an integral, definite or indefinite, we always add , as there could be a constant involved.

$\int x^3+2x+5{\mathrm{d} x}=\frac{x^{4}}{4}+\frac{2x^{2}}{2}+\frac{5x^{1}}{1}+c$

$\int x^3+2x+5{\mathrm{d} x}=\frac{1}{4}x^4+x^2+5x+c$

Plug that back into the FTOC:

$\int_a^b x^3+2x+5{\mathrm{d} x}=(\frac{1}{4}b^4+b^2+5b+c)-(\frac{1}{4}a^4+a^2+5a+c)$

Notice that the 's cancel out.

Plug in our given values from the problem.

$\int_4^5 x^3+2x+5{\mathrm{d} x}=(\frac{1}{4}(5)^4+(5)^2+5(5))-(\frac{1}{4}(4)^4+(4)^2+5(4))$ $\int_4^5 x^3+2x+5{\mathrm{d} x}=(\frac{1}{4}*625+25+25)-(\frac{1}{4}*256+16+20)$

$\int_4^5 x^3+2x+5{\mathrm{d} x}=(156.25+25+25)-(64+16+20)$

$\int_4^5 x^3+2x+5{\mathrm{d} x}=(206.25)-(100)$

$\int_4^5 x^3+2x+5{\mathrm{d} x}=106.25$

Report an Error

Example Question #11 : Integrals

$\int_4^8 6x^2+8{\mathrm{d} x}=?$

Possible Answers:

1088

160

928

1488

1248

Correct answer:

928

Explanation:

Use the Fundamental Theorem of Calculus: If g'(x)=f(x) , then $\int_a^bf(x)=g(b)-g(a)$ .

Therefore, we need to find the indefinite integral of our equation first.

To do that, we can use the anti-power rule or reverse power rule. We raise the exponent on the variables by one and divide by the new exponent.

For this problem, we'll treat as 8x^0 since anything to the zero power is one.

$\int 6x^2+8{\mathrm{d} x}=\frac{6x^{2+1}}{2+1}+\frac{8x^{0+1}}{0+1}+c$

Since the derivative of any constant is , when we take the indefinite integral, we add a to compensate for any constant that might be there.

From here we can simplify.

$\int 6x^2+8{\mathrm{d} x}=\frac{6x^{3}}{3}+\frac{8x^{1}}{1}+c$

$\int 6x^2+8{\mathrm{d} x}=2x^3+8x+c$

That means that $\int_a^b6x^2+8{\mathrm{d} x}=(2b^3+8b+c)-(2a^3+8a+c)$ .

Notice that the 's cancel out.

From here, plug in our numbers.

$\int_4^86x^2+8{\mathrm{d} x}=(2(8)^3+8(8))-(2(4)^3+8(4))$

$\int_4^86x^2+8{\mathrm{d} x}=(2*512+64)-(2*64+32)$

$\int_4^86x^2+8{\mathrm{d} x}=(1024+64)-(128+32)$

$\int_4^86x^2+8{\mathrm{d} x}=(1088)-(160)$

$\int_4^86x^2+8{\mathrm{d} x}=928$

Report an Error

Example Question #311 : Ap Calculus Ab

$\int_2^{12} x+1{\mathrm{d} x}=?$

Possible Answers:

Correct answer:

Explanation:

Use the Fundamental Theorem of Calculus: If g'(x)=f(x) , then $\int_a^bf(x)=g(b)-g(a)$ .

Therefore, we need to find the indefinite integral of our equation first.

To do that, we can use the anti-power rule or reverse power rule. We raise the exponent on the variables by one and divide by the new exponent.

For this problem, we'll treat as 1x^0 since anything to the zero power is one.

$\int x+1{\mathrm{d} x}=\frac{x^{1+1}}{1+1}+\frac{1x^{0+1}}{0+1}+c$

Since the derivative of any constant is , when we take the indefinite integral, we add a to compensate for any constant that might be there.

From here we can simplify.

$\int x+1{\mathrm{d} x}=\frac{x^{2}}{2}+\frac{x^{1}}{1}+c$

$\int x+1{\mathrm{d} x}=\frac{1}{2}x^2+x+c$

According to FTOC:

$\int_a^b x+1{\mathrm{d} x}=(\frac{1}{2}b^2+b+c)-(\frac{1}{2}a^2+a+c)$

Notice that the 's cancel out.

Plug in our given information and solve.

$\int_2^{12} x+1{\mathrm{d} x}=(\frac{1}{2}(12)^2+(12))-(\frac{1}{2}(2)^2+(2))$

$\int_2^{12} x+1{\mathrm{d} x}=(\frac{1}{2}*144+12)-(\frac{1}{2}*4+2)$

$\int_2^{12} x+1{\mathrm{d} x}=(72+12)-(2+2)$

$\int_2^{12} x+1{\mathrm{d} x}=(84)-(4)$

$\int_2^{12} x+1{\mathrm{d} x}=80$

Report an Error

Example Question #101 : Functions, Graphs, And Limits

$\int_3^512x^2+13x+4{\mathrm{d} x}=?$

Possible Answers:

178.5

504

682.5

Undefined

861

Correct answer:

504

Explanation:

Use the Fundamental Theorem of Calculus: If g'(x)=f(x) , then $\int_a^bf(x)=g(b)-g(a)$ .

Therefore, we need to find the indefinite integral of our equation first.

To do that, we can use the anti-power rule or reverse power rule. We raise the exponent on the variables by one and divide by the new exponent.

For this problem, we'll treat as 4x^0 since anything to the zero power is one.

$\int 12x^2+13x+4{\mathrm{d} x}=\frac{12x^{2+1}}{2+1}+\frac{13x^{1+1}}{1+1}+\frac{4x^{0+1}}{0+1}+c$

Since the derivative of any constant is , when we take the indefinite integral, we add a to compensate for any constant that might be there.

From here we can simplify.

$\int 12x^2+13x+4{\mathrm{d} x}=\frac{12x^{3}}{3}+\frac{13x^{2}}{2}+\frac{4x^{1}}{1}+c$

$\int 12x^2+13x+4{\mathrm{d} x}=4x^3+\frac{13}{2}x^2+4x+c$

According to FTOC:

$\int_a^b 12x^2+13x+4{\mathrm{d} x}=(4b^3+\frac{13}{2}b^2+4b+c)-(4a^3+\frac{13}{2}a^2+4a+c)$

Notice that the 's cancel out.

Plug in our given numbers and solve.

$\int_3^5 12x^2+13x+4{\mathrm{d} x}=(4(5)^3+\frac{13}{2}(5)^2+4(5))-(4(3)^3+\frac{13}{2}(3)^2+4(3))$

$\int_3^5 12x^2+13x+4{\mathrm{d} x}=((4*125)+(\frac{13}{2}*25)+20)-((4*27)+(\frac{13}{2}*(9))+12)$

$\int_3^5 12x^2+13x+4{\mathrm{d} x}=(500+162.5+20)-(108+58.5+12)$

$\int_3^5 12x^2+13x+4{\mathrm{d} x}=(682.5)-(178.5)$

$\int_3^5 12x^2+13x+4{\mathrm{d} x}=504$

Report an Error

Example Question #79 : Comparing Relative Magnitudes Of Functions And Their Rates Of Change

$\int_2^42x^4+\frac{1}{2}x{\mathrm{d} x}=?$

Possible Answers:

427.4

Undefined

399.8

413.6

Correct answer:

399.8

Explanation:

Use the Fundamental Theorem of Calculus. If g'(x)=f(x) , then $\int_a^bf(x)=g(b)-g(a)$ .

Therefore, we need to find the indefinite integral of our equation.

To find the indefinite integral, we can use the reverse power rule: we raise the exponent by one and then divide by our new exponent.

$\int 2x^4+\frac{1}{2}x{\mathrm{d} x}=\frac{2x^{4+1}}{4+1}+\frac{\frac{1}{2}x^{1+1}}{1+1}+c$

Remember when taking the indefinite integral to include a to cover any potential constants.

Simplify.

$\int 2x^4+\frac{1}{2}x{\mathrm{d} x}=\frac{2x^{5}}{5}+\frac{\frac{1}{2}x^{2}}{2}+c$

$\int 2x^4+\frac{1}{2}x{\mathrm{d} x}=\frac{2}{5}x^5+\frac{1}{4}x^{2}+c$

Apply the FTOC:

$\int_a^b 2x^4+\frac{1}{2}x{\mathrm{d} x}=(\frac{2}{5}b^5+\frac{1}{4}b^{2}+c)-(\frac{2}{5}a^5+\frac{1}{4}a^{2}+c)$

Notice that the 's cancel out.

Plug in our given numbers and solve.

$\int_2^4 2x^4+\frac{1}{2}x{\mathrm{d} x}=(\frac{2}{5}(4)^5+\frac{1}{4}(4)^{2})-(\frac{2}{5}(2)^5+\frac{1}{4}(2)^{2})$

$\int_2^4 2x^4+\frac{1}{2}x{\mathrm{d} x}=(\frac{2}{5}*1024+\frac{1}{4}*16)-(\frac{2}{5}*32+\frac{1}{4}*4)$

$\int_2^4 2x^4+\frac{1}{2}x{\mathrm{d} x}=(409.6+4)-(12.8+1)$

$\int_2^4 2x^4+\frac{1}{2}x{\mathrm{d} x}=(413.6)-(13.8)$

$\int_2^4 2x^4+\frac{1}{2}x{\mathrm{d} x}=399.8$

Report an Error

Example Question #2201 : High School Math

$\int_3^83x+12{\mathrm{d} x}=?$

Possible Answers:

71.25

49.5

142.5

241.5

192

Correct answer:

142.5

Explanation:

Use the Fundamental Theorem ofCcalculus. If g'(x)=f(x) , then $\int_a^bf(x)=g(b)-g(a)$ .

Therefore, we need to find the indefinite integral of our equation.

To find the indefinite integral, we can use the reverse power rule: we raise the exponent by one and then divide by our new exponent.

We are going to treat as 12x^0 since anything to the zero power is one.

$\int 3x+12{\mathrm{d} x}=\frac{3x^{1+1}}{1+1}+\frac{12x^{0+1}}{0+1}+c$

Remember when taking the indefinite integral to include a to cover any potential constants.

Simplify.

$\int 3x+12{\mathrm{d} x}=\frac{3x^{2}}{2}+\frac{12x^{1}}{1}+c$

$\int 3x+12{\mathrm{d} x}=\frac{3}{2}x^2+12x+c$

Plug that into our Fundamental Theorem of Calculus:

$\int_a^b 3x+12{\mathrm{d} x}=(\frac{3}{2}b^2+12b+c)-(\frac{3}{2}a^2+12a+c)$

Notice that the 's cancel out.

Plug in our given numbers and solve.

$\int_3^8 3x+12{\mathrm{d} x}=(\frac{3}{2}(8)^2+12(8))-(\frac{3}{2}(3)^2+12(3))$

$\int_3^8 3x+12{\mathrm{d} x}=(\frac{3}{2}*64+12(8))-(\frac{3}{2}*9+12(3))$

$\int_3^8 3x+12{\mathrm{d} x}=(96+96)-(13.5+36)$

$\int_3^8 3x+12{\mathrm{d} x}=(192)-(49.5)$

$\int_3^8 3x+12{\mathrm{d} x}=142.5$

Report an Error

Example Question #2202 : High School Math

$\int_3^55x^2+12x{\mathrm{d} x}=?$

Possible Answers:

$259\tfrac{1}{3}$

$358\tfrac{1}{3}$

$250\tfrac{2}{3}$

$457\tfrac{1}{3}$

Correct answer:

$259\tfrac{1}{3}$

Explanation:

Use the Fundamental Theorem of Calculus. If g'(x)=f(x) , then $\int_a^bf(x)=g(b)-g(a)$ .

Therefore we need to find the indefinite integral.

To find the indefinite integral, we use the reverse power rule. That means we raise the exponent on the variables by one and then divide by the new exponent.

$\int 5x^2+12x{\mathrm{d} x}=\frac{5x^{2+1}}{2+1}+\frac{12x^{1+1}}{1+1}+c$

Remember to include a when computing integrals. This is a place holder for any constant that might be in the new expression.

$\int 5x^2+12x{\mathrm{d} x}=\frac{5x^{3}}{3}+\frac{12x^{2}}{2}+c$

$\int 5x^2+12x{\mathrm{d} x}=\frac{5}{3}x^3+\frac{12}{2}x^2+c$

$\int 5x^2+12x{\mathrm{d} x}=\frac{5}{3}x^3+6x^2+c$

Now plug that back into the FTOC:

$\int_a^b 5x^2+12x{\mathrm{d} x}=(\frac{5}{3}b^3+6b^2+c)-(\frac{5}{3}a^3+6a^2+c)$

Notice that the 's cancel out.

Plug in our given numbers.

$\int_3^5 5x^2+12x{\mathrm{d} x}=(\frac{5}{3}(5)^3+6(5)^2)-(\frac{5}{3}(3)^3+6(3)^2)$

$\int_3^5 5x^2+12x{\mathrm{d} x}=(\frac{5}{3}(125)+6(25))-(\frac{5}{3}(27)+6(9))$

$\int_3^5 5x^2+12x{\mathrm{d} x}=(208\tfrac{1}{3}+150)-(45+54)$

$\int_3^5 5x^2+12x{\mathrm{d} x}=(358\tfrac{1}{3})-(99)$

$\int_3^5 5x^2+12x{\mathrm{d} x}=259\tfrac{1}{3}$

Report an Error

Example Question #2203 : High School Math

$\int_0^4-8x^2+15=?$

Possible Answers:

$-230\tfrac{2}{3}$

$-110\tfrac{2}{3}$

$230\tfrac{2}{3}$

569

Correct answer:

$-110\tfrac{2}{3}$

Explanation:

Use the Fundamental Theorem of Calculus. If g'(x)=f(x) , then $\int_a^bf(x)=g(b)-g(a)$ .

Therefore we need to find the indefinite integral.

To find the indefinite integral, we use the reverse power rule. That means we raise the exponent on the variables by one and then divide by the new exponent.

$\int -8x^2+15{\mathrm{d} x}=\frac{-8x^{2+1}}{2+1}+\frac{15x^{0+1}}{0+1}+c$

Remember to include a when computing integrals. This is a place holder for any constant that might be in the new expression.

$\int -8x^2+15{\mathrm{d} x}=\frac{-8x^{3}}{3}+\frac{15x^{1}}{1}+c$

$\int -8x^2+15{\mathrm{d} x}=-\frac{8}{3}x^3+15x+c$

Plug that back into FTOC:

$\int_a^b -8x^2+15{\mathrm{d} x}=(-\frac{8}{3}b^3+15b+c)-(-\frac{8}{3}a^3+15a+c)$

Notice that the 's cancel out.

Plug in our given numbers.

$\int_0^4 -8x^2+15{\mathrm{d} x}=(-\frac{8}{3}(4)^3+15(4))-(-\frac{8}{3}(0)^3+15(0))$ $\int_0^4 -8x^2+15{\mathrm{d} x}=(-\frac{8}{3}(64)+(60))-(0+0)$

$\int_0^4 -8x^2+15{\mathrm{d} x}=(-170\tfrac{2}{3}+(60))$

$\int_0^4 -8x^2+15{\mathrm{d} x}=-110\tfrac{2}{3}$

Report an Error

Example Question #2204 : High School Math

$\int_3^4x^3+2x^2+5=?$

Possible Answers:

$53\tfrac{1}{4}$

$179\tfrac{7}{12}$

$73\tfrac{5}{12}$

$126\tfrac{2}{3}$

Correct answer:

$73\tfrac{5}{12}$

Explanation:

The Fundamental Theorem of Calculus states that if g'(x)=f(x) , then $\int_a^bf(x)=g(b)-g(a)$ . Therefore, we need to find the indefinite integral of our given equation.

To find the indefinite integral, we can use the reverse power rule. Raise the exponent of the variable by one and then divide by that new exponent.

We're going to treat as 5x^0 .

$\int x^3+2x^2+5{\mathrm{d} x}=\frac{x^{3+1}}{3+1}+\frac{2x^{2+1}}{2+1}+\frac{5x^{0+1}}{0+1}+c$

Remember to include the when taking the integral to compensate for any constant.

$\int x^3+2x^2+5{\mathrm{d} x}=\frac{x^{4}}{4}+\frac{2x^{3}}{3}+\frac{5x^{1}}{1}+c$

Simplify.

$\int x^3+2x^2+5{\mathrm{d} x}=\frac{1}{4}x^4+\frac{2}{3}x^3+5x+c$

Plug that into FTOC:

$\int_a^b x^3+2x^2+5{\mathrm{d} x}=(\frac{1}{4}(b)^4+\frac{2}{3}(b)^3+5(b)+c)-(\frac{1}{4}(a)^4+\frac{2}{3}(a)^3+5(a)+c)$

Notice that the 's cancel out.

Plug in our given numbers.

$\int_3^4 x^3+2x^2+5{\mathrm{d} x}=(\frac{1}{4}(4)^4+\frac{2}{3}(4)^3+5(4))-(\frac{1}{4}(3)^4+\frac{2}{3}(3)^3+5(3))$ $\int_3^4 x^3+2x^2+5{\mathrm{d} x}=(\frac{1}{4}(256)+\frac{2}{3}(64)+20)-(\frac{1}{4}(81)+\frac{2}{3}(27)+15)$

$\int_3^4 x^3+2x^2+5{\mathrm{d} x}=(64+42\tfrac{2}{3}+20)-(20\tfrac{1}{4}+18+15)$

$\int_3^4 x^3+2x^2+5{\mathrm{d} x}=(126\tfrac{2}{3})-(53\tfrac{1}{4})$

$\int_3^4 x^3+2x^2+5{\mathrm{d} x}=73\tfrac{5}{12}$

Report an Error

View Tutors

Artinese
Certified Tutor

University of Maine, Bachelor in Arts, Criminal Justice.

View Tutors

Jimmie
Certified Tutor

Grand Canyon University, Masters in Education, Education.

View Tutors

Rachel
Certified Tutor

Grand Canyon University, Bachelor of Science, Mathematics Teacher Education. Grand Canyon University, Master of Science, Addi...

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

English Tutors in Boston, MCAT Tutors in Washington DC, Computer Science Tutors in Chicago, Computer Science Tutors in Washington DC, LSAT Tutors in Boston, ISEE Tutors in Miami, SAT Tutors in Atlanta, Chemistry Tutors in Phoenix, SAT Tutors in Phoenix, French Tutors in New York City

Popular Courses & Classes

SAT Courses & Classes in Phoenix, Spanish Courses & Classes in Atlanta, GRE Courses & Classes in New York City, MCAT Courses & Classes in Los Angeles, ACT Courses & Classes in Atlanta, GRE Courses & Classes in Philadelphia, GMAT Courses & Classes in San Francisco-Bay Area, GMAT Courses & Classes in Seattle, Spanish Courses & Classes in Los Angeles, MCAT Courses & Classes in Atlanta

Popular Test Prep

MCAT Test Prep in Houston, ISEE Test Prep in Washington DC, MCAT Test Prep in Atlanta, ISEE Test Prep in Miami, ISEE Test Prep in Philadelphia, GRE Test Prep in New York City, GMAT Test Prep in Seattle, SSAT Test Prep in Chicago, SSAT Test Prep in Atlanta, SAT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Calculus II — Integrals

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #15 : Finding Integrals

Example Question #91 : Asymptotic And Unbounded Behavior

Example Question #11 : Integrals

Example Question #311 : Ap Calculus Ab

Example Question #101 : Functions, Graphs, And Limits

Example Question #79 : Comparing Relative Magnitudes Of Functions And Their Rates Of Change

Example Question #2201 : High School Math

Example Question #2202 : High School Math

Example Question #2203 : High School Math

Example Question #2204 : High School Math

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: