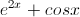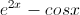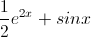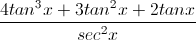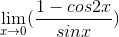Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Calculus II — Integrals

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #11 : Vector

Find the magnitude of v=6i-6j .

Possible Answers:

$\sqrt{24}$

$\sqrt{36}$

$6\sqrt{2}$

Correct answer:

$6\sqrt{2}$

Explanation:

v=6i-6j therefore the vector is <6,-6>

To solve for the magnitude:

$\sqrt{(6)^2+(-6)^2}$

$\sqrt{(36)+(36)}$

$\sqrt{72}$

$6\sqrt{2}$

Report an Error

Example Question #22 : Calculus Ii — Integrals

Let $\vec{}$ $\vec{a}$ and $\vec{b}$ be the following vectors: $\vec{a}=\left \langle 1,2,1\right \rangle$ and $\vec{b}=\left \langle 2,3,-1\right \rangle$ . If $\theta$ is the acute angle between the vectors, then which of the following is equal to $\theta$ ?

Possible Answers:

$\cos^{-1}\left(\frac{\sqrt{21}}{14}\right)$

$\sin^{-1}\left(\frac{\sqrt{21}}{7}\right)$

$\tan^{-1}\left(\frac{\sqrt{21}}{14}\right)$

$\cos^{-1}\left(\frac{\sqrt{21}}{7}\right)$

Correct answer:

$\cos^{-1}\left(\frac{\sqrt{21}}{14}\right)$

Explanation:

The cosine of the acute angle between two vectors is given by the following formula:

$\cos\theta=\frac{\vec{a}\cdot \vec{b}}{\left \| \vec{a}\right \| \left \| \vec{b} \right \|}$ , where $\vec{a} \cdot \vec{b}$ represents the dot product of the two vectors, $\left \| \vec{a} \right \|$ is the magnitude of vector a, and $\left \| \vec{b} \right \|$ is the magnitude of vector b.

First, we will need to compute the dot product of the two vectors. Let's say we have two general vectors in space (three dimensions), $\vec{a}$ and $\vec{b}$ . Let the components of $\vec{a}$ be $<a_{1}, a_{2}, a_{3}>$ and the components of $\vec{b}$ be $<b_{1}, b_{2}, b_{3}>$ . Then the dot product $\vec{a} \cdot \vec{b}$ is defined as follows:

$\vec{a} \cdot \vec{b}=a_{1}(b_{1})+a_{2}(b_{2})+a_{3}(b_{3})$ .

Going back to the original problem, we can use this definition to find the dot product of $\vec{a}=<1,2,1>$ and $\vec{b}=<-2,3,-1>$ .

$\vec{a} \cdot \vec{b}=a_{1}(b_{1})+a_{2}(b_{2})+a_{3}(b_{3})$

=1(-2)+2(3)+1(-1)

=-2+6-1=3

The next two things we will need to compute are $\left \| \vec{a} \right \|$ and $\left \| \vec{b} \right \|$ .

Let the components of a general vector $\vec{a}$ be $<a_{1}, a_{2}, a_{3}>$ . Then $\left \| \vec{a} \right \|$ is defined as $\left \| \vec{a}\right \|=\sqrt{(a_{1})^2+(a_{2})^2+(a_3)^2}$ .

Thus, if $\vec{a}=<1,2,1>$ and $\vec{b}=<-2,3,-1>$ , then

$\left \| \vec{a}\right \|=\sqrt{(a_{1})^2+(a_{2})^2+(a_3)^2}$

$=\sqrt{(1)^2+(2)^2+(1)^2}=\sqrt{1+4+1}=\sqrt{6}$

and $\left \| \vec{b}\right \|=\sqrt{(b_{1})^2+(b_{2})^2+(b_3)^2}=\sqrt{(-2)^2+(3)^2+(-1)^2}$

$=\sqrt{4+9+1}=\sqrt{14}$ .

Now, we put all of this information together to find the cosine of the angle between the two vectors.

$\cos\theta=\frac{\vec{a}\cdot \vec{b}}{\left \| \vec{a}\right \| \left \| \vec{b} \right \|}=\frac{3}{\sqrt{6}\cdot\sqrt{14}}$

We just need to simplify this.

$\frac{3}{\sqrt{6}\cdot\sqrt{14}}=\frac{3}{\sqrt{6\cdot14}}=\frac{3}{\sqrt{2\cdot3\cdot2\cdot7}}$

$=\frac{3}{2\sqrt{21}}$ .

In order to get it completely simplified, we have to rationalize the denominator by multiplying the numerator and denominator by the sqare root of 21.

$\frac{3}{2\sqrt{21}}=\frac{3\cdot\sqrt{21}}{2\sqrt{21}\cdot\sqrt{21}}=\frac{3\sqrt{21}}{2(21)}$

$=\frac{\sqrt{21}}{2\cdot7}=\frac{\sqrt{21}}{14}$ .

We just have one more step. We need to solve for the value of the angle. In order to do this, we can take the inverse cosine of both sides of the equation.

$\cos\theta=\frac{\sqrt{21}}{14}$

$\theta=\cos^{-1}(\frac{\sqrt{21}}{14})$ .

The answer is $\cos^{-1}(\frac{\sqrt{21}}{14})$ .

Report an Error

Example Question #21 : Calculus Ii — Integrals

Find the second derivative of f(x).

$f(x)=\frac{1}{4} e^{2x}-cosx$

Possible Answers:

$\frac{1}{2}e^{2x}+cosx$

$e^{2x}-cosx$

$e^{2x}+sinx$

$e^{2x}+cosx$

$\frac{1}{2}e^{2x}+sinx$

Correct answer:

$e^{2x}+cosx$

Explanation:

First we should find the first derivative of f(x) . Remember the derivative of $e^{2x}$ is $2e^{2x}$ and the derivative of cosx is -sinx :

$f'(x)=\frac{1}{2}e^{2x}+sinx$

The second derivative is just the derivative of the first derivative:

$f''(x)=e^{2x}+cosx$

Report an Error

Example Question #22 : Calculus Ii — Integrals

Find the derivative of the function

f(x)=tan^4x-tan^3x+tan^2x .

Possible Answers:

$(4tan^3x-3tan^2x+2tanx)\cdot csc^2x$

$(4tan^3x-3tan^2x+2tanx)\cdot sec^2x$

$(4tan^3x-3tan^2x+2tanx)\cdot secx$

$\frac{4tan^3x+3tan^2x+2tanx}{sec^2x}$

$\frac{4tan^3x-3tan^2x+2tanx}{csc^2x}$

Correct answer:

$(4tan^3x-3tan^2x+2tanx)\cdot sec^2x$

Explanation:

We can use the Chain Rule:

Let u=tanx , so that f(x)=u^4-u^3+u^2 .

$\frac{df}{dx}=\frac{df}{du}.\frac{du}{dx}=(4u^3-3u^2+2u)\cdot sec^2x=(4tan^3x-3tan^2x+2tanx)\cdot sec^2x$

Report an Error

Example Question #1 : Derivative Interpreted As An Instantaneous Rate Of Change

Evaluate the following limit:

$\lim_{x\rightarrow 0} (\frac{1-cos2x}{sinx})$

Possible Answers:

$\infty$

Correct answer:

Explanation:

When approaches 0 both sinx and (1-cos2x) will approach . Therefore, L’Hopital’s Rule can be applied here. Take the derivatives of the numerator and denominator and try the limit again:

$\lim_{x\rightarrow 0} (\frac{1-cos2x}{sinx})= \lim_{x\rightarrow 0} (\frac{2sin2x}{cosx})=\frac{0}{1}=0$

Report an Error

Example Question #21 : Calculus Ii — Integrals

Evaluate:

$\int_{1}^{e^{100}} \frac{1}{x}dx$

Possible Answers:

$\frac{1}{100}$

$\ln 100$

100e

$\frac{100}{e}$

100

Correct answer:

100

Explanation:

$\int_{1}^{e^{100}} \frac{dx}{x} = \ln e^{100} - \ln 1 = 100-0 = 100$

Report an Error

Example Question #22 : Calculus Ii — Integrals

Find $\int_{0}^{\pi} (\cos^{2}x+\sin^{2}x)dx$

Possible Answers:

$\pi$

$2\pi$

Correct answer:

$\pi$

Explanation:

This is most easily solved by recognizing that $\sin^{2}x+\cos^{2}x=1$ .

Report an Error

Example Question #21 : Calculus Ii — Integrals

$\int_{\pi}^{2\pi}\sin(2x){\mathrm{d} x}=?$

Possible Answers:

$\pi$

$\frac{1}{2}$

Correct answer:

Explanation:

Remember the fundamental theorem of calculus!

$\int_{a}^{b}f(x){\mathrm{d} x}=\int f(b){\mathrm{d} x}-\int f(a){\mathrm{d} x}$

Since our $f(x)=\sin(2x)$ , we can't use the power rule. Instead we end up with:

$\int f(x){\mathrm{d} x}=\int \sin(2x){\mathrm{d} x}=\frac{-\cos(2x)}{2}+c$

Remember to include the + c for any anti-derivative or integral taken!

Now we can plug that equation into our FToC equation:

$\int_{a}^{b}f(x){\mathrm{d} x}=(\frac{-\cos(2b)}{2}+c)-(\frac{-\cos(2a)}{2}+c)$

Notice that the c's cancel out. Plug in the given values for a and b and solve:

$\int_{\pi}^{2\pi}f(x){\mathrm{d} x}=(\frac{-\cos(4\pi)}{2})-(\frac{-\cos(2\pi)}{2})$

$\int_{\pi}^{2\pi}f(x){\mathrm{d} x}=(\frac{-1}{2})-(\frac{-1}{2})$

$\int_{\pi}^{2\pi}f(x){\mathrm{d} x}=0$

Report an Error

Example Question #1 : Finding Definite Integrals

$\int_{2}^{4}x^2{\mathrm{d} x}=?$

Possible Answers:

$11\tfrac{3}{4}$

$5\tfrac{1}{2}$

$18\frac{2}{3}$

$28\tfrac{2}{3}$

$22\tfrac{1}{3}$

Correct answer:

$18\frac{2}{3}$

Explanation:

Remember the fundamental theorem of calculus!

$\int_{a}^{b}f(x){\mathrm{d} x}=\int f(b){\mathrm{d} x}-\int f(a){\mathrm{d} x}$

Since our f(x)=x^2 , we can use the reverse power rule to find the indefinite integral or anti-derivative of our function:

$\int (x^2){\mathrm{d} x}=\frac{1}{3}x^3+c$

Remember to include the + c for any anti-derivative or integral taken!

Now we can plug that equation into our FToC equation:

$\int_{a}^{b}f(x){\mathrm{d} x}=(\frac{1}{3}b^3+c)-(\frac{1}{3}a^3+c)$

Notice that the c's cancel out. Plug in the given values for a and b and solve:

$\int_{2}^{4}f(x){\mathrm{d} x}=(\frac{1}{3}\cdot 4^3)-(\frac{1}{3}\cdot 8^3)$

$\int_{2}^{4}f(x){\mathrm{d} x}=(\frac{64}{3})-(\frac{8}{3})$

$\int_{2}^{4}f(x){\mathrm{d} x}=\frac{56}{3}=18\frac{2}{3}$

Report an Error

Example Question #43 : Comparing Relative Magnitudes Of Functions And Their Rates Of Change

$\int_{1}^{2}\frac{1}{x}{\mathrm{d} x}=?$

Possible Answers:

0.81

1.2

0.30

0.75

0.69

Correct answer:

0.69

Explanation:

Remember the fundamental theorem of calculus!

$\int_{a}^{b}f(x){\mathrm{d} x}=\int f(b){\mathrm{d} x}-\int f(a){\mathrm{d} x}$

As it turns out, since our $f(x)=\frac{1}{x}$ , the power rule really doesn't help us. $\frac{1}{x}$ has a special anti derivative: $\ln{x}$ .

$\int \frac{1}{x}{\mathrm{d} x}=\ln{x}+c$

Remember to include the + c for any anti-derivative or integral taken!

Now we can plug that equation into our FToC equation:

$\int_{a}^{b}f(x){\mathrm{d} x}=(\ln{b}+c)-(\ln{a}+c)$

Notice that the c's cancel out. Plug in the given values for a and b and solve:

$\int_{1}^{2}f(x){\mathrm{d} x}=(\ln(2))-(\ln(1))$

$\int_{1}^{2}f(x){\mathrm{d} x}=(\ln(2))-(0)$

$\int_{1}^{2}f(x){\mathrm{d} x}\approx 0.69$

Report an Error

View Tutors

Donald
Certified Tutor

Cleveland State University, Bachelor of Science, Chemistry. University of Southern California, Doctor of Philosophy, Organic ...

View Tutors

Victoria
Certified Tutor

Norte Dame de Namur University, Bachelor in Arts, Sociology. University of San Francisco, Master of Arts, Organizational Lead...

View Tutors

Shweta
Certified Tutor

All India Management Association , Master's/Graduate, Human Resource Management . Indian Law Institute , Master's/Graduate, C...

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GRE Tutors in Washington DC, Computer Science Tutors in Dallas Fort Worth, Algebra Tutors in Denver, Math Tutors in Boston, Math Tutors in Philadelphia, Algebra Tutors in Houston, GMAT Tutors in Philadelphia, Math Tutors in San Francisco-Bay Area, Calculus Tutors in Seattle, Computer Science Tutors in Phoenix

Popular Courses & Classes

MCAT Courses & Classes in Los Angeles, MCAT Courses & Classes in San Diego, Spanish Courses & Classes in Washington DC, MCAT Courses & Classes in Denver, SAT Courses & Classes in Washington DC, ACT Courses & Classes in Miami, MCAT Courses & Classes in Atlanta, LSAT Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Los Angeles, LSAT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

ACT Test Prep in Miami, SSAT Test Prep in Chicago, SSAT Test Prep in Philadelphia, GRE Test Prep in Seattle, MCAT Test Prep in Washington DC, MCAT Test Prep in Boston, ISEE Test Prep in Boston, ISEE Test Prep in Miami, GRE Test Prep in San Diego, GRE Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Calculus II — Integrals

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #11 : Vector

Example Question #22 : Calculus Ii — Integrals

Example Question #21 : Calculus Ii — Integrals

Example Question #22 : Calculus Ii — Integrals

Example Question #1 : Derivative Interpreted As An Instantaneous Rate Of Change

Example Question #21 : Calculus Ii — Integrals

Example Question #22 : Calculus Ii — Integrals

Example Question #21 : Calculus Ii — Integrals

Example Question #1 : Finding Definite Integrals

Example Question #43 : Comparing Relative Magnitudes Of Functions And Their Rates Of Change

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: