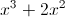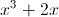Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Algebra II

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Multiplying And Dividing Exponents

Simplify the following expression.

$2^{3} \cdot 2^{6}$

Possible Answers:

$6^{6}$

$4^{9}$

$4^{18}$

$2^{18}$

$2^{9}$

Correct answer:

$2^{9}$

Explanation:

We are given: $2^{3} \cdot 2^{6}$ .

Recall that when we are multiplying exponents with the same base, we keep the base the same and add the exponents.

Thus, we have $2^{3 + 6} = 2^{9}$ .

Report an Error

Example Question #1 : Multiplying And Dividing Exponents

Simplify the following expression.

$\frac{2^{9}}{2^{11}}$

Possible Answers:

$2^{\frac{9}{11}}$

$2^{2}$

$\frac{1}{2^{2}}$

$\frac{18}{22}$

$\frac{9}{11}$

Correct answer:

$\frac{1}{2^{2}}$

Explanation:

Recall that when we are dividing exponents with the same base, we keep the base the same and subtract the exponents.

Thus, we have $\frac{2^{9}}{2^{11}} = 2^{9 - 11} = 2^{-2}$ .

We also recall that for negative exponents,

$b^{-x} = \frac{1}{b^{x}}$ .

Thus, $2^{-2} = \frac{1}{2^{2}}$ .

Report an Error

Example Question #1 : Multiplying And Dividing Exponents

Simplify the following exponent expression:

$(\frac{a^{\frac{-3}{2}}}{3^6b^{\frac{-2}{3}}})^{\frac{-1}{2}}$

Possible Answers:

$\frac{a^{\frac{3}{4}}}{b^{\frac{1}{3}}}$

$\frac{27a^{\frac{3}{4}}}{b^{\frac{1}{3}}}$

$\frac{9a^{\frac{3}{4}}}{b^{\frac{1}{3}}}$

$\frac{3a^{\frac{3}{4}}}{b^{\frac{1}{3}}}$

$\frac{18a^{\frac{3}{4}}}{b^{\frac{1}{3}}}$

Correct answer:

$\frac{27a^{\frac{3}{4}}}{b^{\frac{1}{3}}}$

Explanation:

Begin by rearranging the terms in the numerator and denominator so that the exponents are positive:

$(\frac{a^{\frac{-3}{2}}}{3^6b^{\frac{-2}{3}}})^{\frac{-1}{2}}$

$(\frac{3^6b^{\frac{-2}{3}}}{a^{\frac{-3}{2}}})^{\frac{1}{2}}$

$(\frac{3^6a^{\frac{3}{2}}}{b^{\frac{2}{3}}})^{\frac{1}{2}}$

Multiply the exponents:

$(\frac{3^3a^{\frac{3}{4}}}{b^{\frac{1}{3}}})$

Simplify:

$\frac{27a^{\frac{3}{4}}}{b^{\frac{1}{3}}}$

Report an Error

Example Question #1 : Simplifying Exponents

Simplify the expression:

$x^3 + \frac{2x^2}{x^{-1}}$

Possible Answers:

$x^3+\frac{2}{x^3}$

x^3+2

x^3+2x

x^3+2x^2

3x^3

Correct answer:

3x^3

Explanation:

First simplify the second term, and then combine the two:

$x^3 + \frac{2x^2}{x^{-1}}$

$= x^3 + 2x^{2-(-1)} = x^3 + 2x^3 = 3x^3$

Report an Error

Example Question #1 : Multiplying And Dividing Exponents

Solve for : 4^y = 32*2^2^y^-^x

Possible Answers:

x=0

x=3

x=-3

x=5

Cannot be determined from the given information.

Correct answer:

x=5

Explanation:

Rewrite each side of the equation to only use a base 2:

$2^{2y} = 2^{5}*2^{2y-x}$

$2^{2y} = 2^{5+2y-x}$

The only way this equation can be true is if the exponents are equal.

So:

2y = 5+2y-x

The on each side cancel, and moving the to the left side, we get:

x=5

Report an Error

Example Question #1 : Simplifying Exponents

$\log_{x}27e^{3}=3$

Solve for .

Possible Answers:

1/2e

Correct answer:

Explanation:

First, set up the equation: x^3=27 e^3 . Simplifying this result gives x = 3 .

Report an Error

Example Question #2 : Simplifying Exponents

What is the largest positive integer, , such that 2^z is a factor of 16^4 ?

Possible Answers:

Correct answer:

Explanation:

16^4 = (2^4)^4 = 2^1^6 . Thus, is equal to 16.

Report an Error

Example Question #1 : Distributing Exponents (Power Rule)

Order the following from least to greatest:

$25^{100}$

$2^{300}$

$3^{500}$

$4^{400}$

$2^{600}$

Possible Answers:

$3^{500}, 4^{400}, 2^{300}, 25^{100}, 2^{600}$

$2^{600}, 2^{300}, 25^{100}, 3^{500}, 4^{400}$

$2^{300}, 25^{100}, 2^{600}, 3^{500}, 4^{400}$

$2^{300}, 2^{600}, 3^{500}, 25^{100}, 4^{400}$

$25^{100}, 2^{300}, 2^{600}, 3^{500}, 4^{400}$

Correct answer:

$2^{300}, 25^{100}, 2^{600}, 3^{500}, 4^{400}$

Explanation:

In order to solve this problem, each of the answer choices needs to be simplified.

Instead of simplifying completely, make all terms into a form such that they have 100 as the exponent. Then they can be easily compared.

2^3^0^0 = (2^3)^1^0^0 = 8^1^0^0 , 3^5^0^0 = (3^5)^1^0^0 = 243^1^0^0 , 4^4^0^0 = (4^4)^1^0^0 = 256^1^0^0 , and 2^6^0^0 = (2^6)^1^0^0 = 64^1^0^0 .

Thus, ordering from least to greatest: 8^1^0^0, 25^1^0^0, 64^1^0^0, 243^1^0^0, 256^1^0^0 .

Report an Error

Example Question #1 : Review And Other Topics

Simplify the expression:

$(3x^4y^2)(4xy^2)^{-3}$

Possible Answers:

$\frac{3x}{64y^3}$

Cannot be simplified

$\frac{3x}{16y^3}$

$\frac{3x}{64y^4}$

Correct answer:

$\frac{3x}{64y^4}$

Explanation:

Begin by distributing the exponent through the parentheses. The power rule dictates that an exponent raised to another exponent means that the two exponents are multiplied:

$(3x^{4}y^2)(4xy^2)^{-3}= (3xy^2)(4^{-3}x^{-3}y^{-6})$

Any negative exponents can be converted to positive exponents in the denominator of a fraction:

$\frac{3x^4y^2}{64x^3y^6}$

The like terms can be simplified by subtracting the power of the denominator from the power of the numerator:

$\frac{3x^4y^2}{64x^3y^6}=\frac{3}{64}x^{4-3}y^{2-6}=\frac{3}{64}xy^{-4}$

$\frac{3x}{64y^4}$

Report an Error

Example Question #102 : Mathematical Relationships And Basic Graphs

$y=\frac{x^2-9}{x^2-16}$

What are the y-intercepts of this equation?

Possible Answers:

$y=\frac{16}{9}$

y=0

$y=\frac{9}{16}$

y=3,-3

y=4,-4

Correct answer:

$y=\frac{9}{16}$

Explanation:

To find the y-intercepts, set the value equal to and solve.

$y=\frac{x^2-9}{x^2-16}$

$y=\frac{(0)^2-9}{(0)^2-16}$

$y=\frac{-9}{-16}$

$y=\frac{9}{16}$

Report an Error

View Tutors

Lisa
Certified Tutor

Rockefeller University, Master of Public Policy, Public Policy Analysis.

View Tutors

Lisa
Certified Tutor

University of Toronto, Bachelor of Science, Psychology. University of Tornoto, Bachelor in Arts, Anthropology.

View Tutors

Tracy
Certified Tutor

Florida Memorial University, Bachelor in Arts, English.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Statistics Tutors in Boston, MCAT Tutors in Houston, Computer Science Tutors in Denver, Algebra Tutors in Atlanta, Algebra Tutors in Miami, LSAT Tutors in Seattle, Biology Tutors in Philadelphia, Algebra Tutors in New York City, English Tutors in Atlanta, ISEE Tutors in New York City

Popular Courses & Classes

SAT Courses & Classes in Phoenix, SSAT Courses & Classes in San Francisco-Bay Area, GMAT Courses & Classes in Washington DC, SSAT Courses & Classes in New York City, SAT Courses & Classes in Boston, SAT Courses & Classes in New York City, SAT Courses & Classes in Atlanta, ISEE Courses & Classes in Boston, MCAT Courses & Classes in Denver, SAT Courses & Classes in Chicago

Popular Test Prep

LSAT Test Prep in Washington DC, GMAT Test Prep in Los Angeles, SAT Test Prep in Miami, SAT Test Prep in Chicago, MCAT Test Prep in Los Angeles, GRE Test Prep in Philadelphia, SAT Test Prep in Seattle, GRE Test Prep in New York City, ISEE Test Prep in Dallas Fort Worth, LSAT Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Algebra II

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : Multiplying And Dividing Exponents

Example Question #1 : Multiplying And Dividing Exponents

Example Question #1 : Multiplying And Dividing Exponents

Example Question #1 : Simplifying Exponents

Example Question #1 : Multiplying And Dividing Exponents

Example Question #1 : Simplifying Exponents

Example Question #2 : Simplifying Exponents

Example Question #1 : Distributing Exponents (Power Rule)

Example Question #1 : Review And Other Topics

Example Question #102 : Mathematical Relationships And Basic Graphs

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: