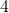In a group of philosophers,  are followers of Durandus. Twice that number are followers of Ockham. Four times the number of followers of Ockham are followers of Aquinas. One sixth of the number of followers of Aquinas are followers of Scotus. How many total philosophers are in the group?

To start, let's calculate the total philosophers:

Ockham:  * <Number following Durandus>, or 

Aquinas:  * <Number following Ockham>, or 

Scotus:  divided by , or 

Therefore, the total number is:

When two even numbers are multiplied, they must equal an even number. Also, since both variables are said to be even whole numbers, the answer must fit the requirement that its factors are two even numbers multiplied by one another. The only answer that fits both requirements is  which can be factored into the even whole numbers  and .

There are certain patterns that can be used to predict whether the product or sum of numbers will be odd or even. The sum of two odd numbers is always even, as is the sum of two even numbers. The sum of an odd number and an even number is always odd. In multiplication the product of two odd numbers is always odd. While the product of even numbers, as well as the product of odd numbers multiplied by even numbers is always even. So for this problem we need to find scenarios where the only possibile answers are even.  can only result in even numbers no matter what positive integers are used for  and , because  must can only result in even products; the same can be said for . The rules provide that the sum of two even numbers is even, so  is the answer.

To solve this problem, set up long division for yourself.  First, you know that your hundreds digit of the solution will be one, as twelve goes into seventeen one time.  Then, you take twelve away from seventeen, and are left with three remaining.  Bring down your next digit over from the dividend, and you are left with thirty two, which twelve goes into four times.  Already, you know that the answer has to be  as none of the other answers fit the correct pattern.

To solve, first isolate the variable by dividing both sides of the equation by :

As a check, know that any time you divide an even number by another even number, you will get an even result. 

To solve, isolate your variable by dividing both sides of the equation by :

As a check, know that any time you divide an even number by another even number, the result will be even. 

To solve, isolate the variable by dividing both sides of the equation by :

As a check, know that any time you divide an even number by another even number, the result will be even.  

To solve, isolate the variable by dividing both sides of your equation by :

As a check, know that any time you divide an even number by another even number, your result will be even. 

Since , then the final answer will be a number greater than one. The only answer that fits is .