All GRE Math Resources
Example Questions
Example Question #3 : Statistics
Find the median:
To find the median, arrange the numbers from smallest to largest:
4,4,4,4,6,7,9,9,12,12,12,12,12,12,18,76,90
There are 17 numbers in total. Since 17 is an odd number, the median will be the middle number of the set. In this case, it is the 9th number, which is 12.
Example Question #1 : How To Find Median
There are 3,500 people in group A and 5,000 people in group B:
|
Car Type |
% in Group A Who Own |
% in Group B Who Own |
|
Motorbike |
4 |
9 |
|
Sedan |
35 |
25 |
|
Minivan |
22 |
15 |
|
Van |
9 |
12 |
|
Coupe |
3 |
6 |
What is the median of the number of people in group B who own either a minivan, van, or coupe?
Treat the percentages as a list, as we are including every demographic from the 3 vehicle types mentioned. If we do each 0.06(5000), 0.12(5000), and 0.15(5000) we note from observation that the median, or middle value, would have to be the 12% row since the sample size does not change. The question asks for EITHER of the 3 categories, so we can ignore the other two.
0.12(5000) = 600 (van) is the median of the 3 categories.
Example Question #4 : Statistics
In the set above, which is larger: the median, the mean, or the mode?
Both median and mean
Mode
All are equal
Mean
Median
Mean
Begin by ordering the set from smallest to largest:
Already, we see that the mode is 8. Find the median by taking the average of the two middle numbers:
Find the mean by adding all numbers and dividing by the total number of terms:
Of the three, the mean of the set is the largest.
Example Question #6 : How To Find Median
The grades on a test taken by 

To solve this problem, we must be aware of the definition of a median for a set of numbers. The median is defined as the number that is in middle of a set of numbers sorted from smallest to largest. Therefore we must first sort the numbers from largest to smallest.
34,43,45,50,56,65,70,76,76,82,87,88,92,95,100
43,45,50,56,65,70,76,76,81,87,88,82,95
45,50,56,65,70,76,76,81,87,88,82
50,56,65,70,76,76,81,87,88
56,65,70,76,76,81,87
65,70,76,76,81
70,76,76
76
Then by slowly eliminating the smallest and the largest numbers we find that the median score for this test is 76.
Example Question #5 : Statistics
Quantity A: The mean of
Quantity B: The median of
Quantity B is greater.
The relationship cannot be determined.
The two quantities are equal.
Quantity A is greater.
Quantity B is greater.
Begin by reordering the set in numerical order:
Then becomes
Since there is an odd number of values, the median is the middle value.
Quantity B:
Now, to find the arithmetic mean, take the sum of values divided by the total number of values.
Quantity A:
Example Question #6 : Statistics
The arithmetic mean of 



Now, 
Since there are even number of values, the median is the mean of the two middle most values:
Example Question #4 : Statistics
Column A
The mean of the sample of numbers 2, 5, and 10.
Column B
The mean of the sample of numbers 1, 5, and 15.
The relationship cannot be determined from the information given.
The quantity in Column B is greater.
The two quantities are equal.
The quantity in Column A is greater.
The quantity in Column B is greater.
The arithmetic mean is the average of the sum of a set of numbers divided by the total number of numbers in the set. This is not to be confused with median or mode.
In Column A, the mean of 5.66 is obtained when the sum (17) is divided by the number of values in the set (3).
In Column B, the mean of 7 is obtained when 21 is divided by 3. Because 7 is greater than 5.66, Column B is greater. The answer is Column B.
Example Question #1 : How To Find Arithmetic Mean
Bill runs for 30 minutes at 8 mph and then runs for 15 minutes at 13mph. What was his average speed during his entire run?
11 mph
101/2 mph
92/3 mph
10 mph
92/3 mph
Rate = distance/time.
Find the distance for each individual segment of the run (4 miles and 3.25miles). Then add total distance and divide by total time to get the average rate, while making sure the units are compatible (miles per hour not miles per minute), which means the total 45 minute run time needs to be converted to 0.75 of an hour; therefore (4miles + 3.25 miles/0.75 hour) is the final answer.
Example Question #2 : How To Find Arithmetic Mean
Sample Set A has 25 data points with an arithmetic mean of 50.
Sample Set B has 75 data points with an arithmetic mean of 100.
Quantity A: The arithmetic mean of the 100 data points encompassing A and B
Quantity B: 80
The two quantities are equal.
Quantity A is greater.
The relationship cannot be determined from the information given.
Quantity B is greater.
Quantity A is greater.
Note that:
The arithmetic mean of the 100 data points encompassing A and B =
(total data of Sample Set A + total data of Sample Set B)/100
We have Mean of Sample Set A = 50, or:
(total of Sample Set A) / 25 = 50
And we have Mean of Sample Set B = 100, or:
(total of Sample Set B) / 75 = 100
We get denominators of 100 by dividing both of the equations:
Divide [(total of Sample Set A) / 25 = 50] by 4:
(total of Sample Set A) / 100 = 50/4 = 25/2
Multiply [(total of Sample Set B)/75 = 100] by 3/4:
(total of Sample Set B)/100 = 75
Now add the two equations together:
(total data of Sample Set A + total data of Sample Set B)/100
Example Question #3 : How To Find Arithmetic Mean
The average (arithmetic mean) of x, y and z is 15. If w is 10, then what is the average of w, x, y and z?
13.75
12.5
10
12.75
15
13.75
We can calculate the arithmetic mean by adding up the numbers in a set, and dividing that total by the count of numbers in the set.
Thus, we know that (x + y + z) / 3 = 15. (Multiply both sides by 3.)
x + y + z = 45
We add w = 10 to that, and divide by the new count, 4.
55 / 4 = 13.75
All GRE Math Resources


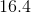
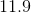

















![Set_A=[-10,4,2,-14,-2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/488996/gif.latex)


![Set_A=[-10,4,2,-14,-2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/488997/gif.latex)
![Set_A=[-14,-10,-2,2,4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/488998/gif.latex)























