GRE Math : GRE Quantitative Reasoning

Study concepts, example questions & explanations for GRE Math

Create An Account

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Length Of The Side Of A Parallelogram

Parallelogram gre

Using the parallelogram shown above, find the length of side

Possible Answers:

Correct answer:

Explanation:

A parallelogram must have two sets of congruent/parallel opposite sides. Therefore, this parallelogram must have two sides with a measurement of and two base sides each with a length of 18. Since the perimeter and one base length is provided in the question, work backwards using the perimeter formula:

$\textup{Perimeter}=2(a+b)$ , where and are the measurements of adjacent sides.

Thus, the solution is:

68=2(18+b)

68=36+2b

2b=68-36=32

$b=\frac{32}{2}=16$

Report an Error

Example Question #1342 : Gre Quantitative Reasoning

A parallelogram has a base of . The perimeter of the parallelogram is . Find the sum of the two adjacent sides to the base.

Possible Answers:

Correct answer:

Explanation:

A parallelogram must have two sets of congruent/parallel opposite sides. This parallelogram must have two sides with a measurement of and two base sides each with a length of . In this question, you are provided with the information that the parallelogram has a base of and a total perimeter of . Thus, work backwards using the perimeter formula in order to find the sum of the two adjacent sides to the base.

$\textup{Perimeter}=2(a+b)$ , where and are the measurements of adjacent sides.

Thus, the solution is:

72=2(22+b)

72=44+2b

2b=72-44=28

Report an Error

Example Question #1343 : Gre Quantitative Reasoning

A parallelogram has a base of . An adjacent side to the base has a length of . Find the perimeter of the parallelogram.

Possible Answers:

47.5

Correct answer:

Explanation:

A parallelogram must have two sets of congruent/parallel opposite sides. Therefore, this parallelogram must have two sides with a measurement of and two base sides each with a length of 28. To find the perimeter of the parallelogram apply the formula:

$\textup{Perimeter}=2(a+b)$ , where and are the measurements of adjacent sides.

Thus, the solution is:

p=2(28+18)

p=2(46)

p=92

Report an Error

Example Question #25 : Quadrilaterals

A parallelogram has a base of $95\textup{mm}$ . The perimeter of the parallelogram is $338\textup{mm}$ . Find the length for an adjacent side to the base.

Possible Answers:

$36\textup{mm}$

$74\textup{mm}$

$148\textup{mm}$

$42\textup{mm}$

$72\textup{mm}$

Correct answer:

$74\textup{mm}$

Explanation:

A parallelogram must have two sets of congruent/parallel opposite sides. Therefore, this parallelogram must have two sides with a measurement of $74\textup{mm}$ and two base sides each with a length of $95\textup{mm}$ . To solve for the missing side, work backwards using the perimeter formula:

$\textup{Perimeter}=2(a+b)$ , where and are the measurements of adjacent sides.

Thus, the solution is:

338=2(95+b)

338=190+2b

2b=338-190=148

$b=\frac{148}{2}=74$

Report an Error

Example Question #1341 : Gre Quantitative Reasoning

A quadrilateral has equal sides, each with a length of .

Quantity A: The area of the quadrilateral.

Quantity B: The perimeter of the quadrilateral.

Possible Answers:

The relationship cannot be determined.

The two quantities are equal.

Quantity A is greater.

Quantity B is greater.

Correct answer:

The relationship cannot be determined.

Explanation:

We are told that the shape is a quadrilateral and that the sides are equal; beyond that, we do not know what specific kind of kind of quadrilateral it is, outside of the fact that it is a rhombus. The perimeter, the sum of the sides, is .

If this shape were a square, the area would also be ; however, if the interior angles were not all equivalent, the area would be smaller than this.

The relationship cannot be determined.

Report an Error

Example Question #151 : Plane Geometry

A rectangle has an area of 48 and a perimeter of 28. What are its dimensions?

Possible Answers:

2 x 24

0.25 x 192

1 x 48

6 x 8

16 x 3

Correct answer:

6 x 8

Explanation:

We can set up our data into the following two equations:

(Area) LH = 48

(Perimeter) 2L + 2H = 28

Solve the area equation for one of the two variables (here, length): L = 48 / H

Place that value for L into ever place you find L in the perimeter equation: 2(48 / H) + 2H = 28; then simplify:

96/H + 2H = 28

Multiply through by H: 96 + 2H² = 28H

Get everything on the same side of the equals sign: 2H² - 28H + 96 = 0

Divide out the common 2: H² - 14H + 48 = 0

Factor: (H - 6) (H - 8) = 0

Either of these multiples can be 0, therefore, consider each one separately:

H - 6 = 0; H = 6

H - 8 = 0; H = 8

Because this is a rectangle, these two dimensions are the height and width. If you choose 6 for the "height" the other perpendicular dimension would be 8 and vice-versa. Therefore, the dimensions are 6 x 8.

Report an Error

Example Question #31 : Quadrilaterals

The length of a rectangle is three times its width, and the perimeter is . What is the width of the rectangle?

Possible Answers:

Correct answer:

Explanation:

For any rectangle, 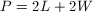$\dpi{100} \small P=2L+2W$ , where $\dpi{100} \small P=perimeter$ , $\dpi{100} \small L=length$ , and $\dpi{100} \small W=width$ .

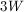
In this problem, we are given that $\dpi{100} \small L=3W$ (length is three times the width), so replace $\dpi{100} \small L$ in the perimeter equation with $\dpi{100} \small 3W$ : $\dpi{100} \small P=2(3W)+2W$

Plug in our value for the perimeter, $\dpi{100} \small P$ :

$\dpi{100} \small 16=2(3W)+2W$

Simplify:

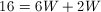
$\dpi{100} \small 16=6W+2W$

$\dpi{100} \small 16=8W$

$\dpi{100} \small W=2$

Report an Error

Example Question #1 : Rectangles

The area of a rectangle is $70\:in^2$ . Its perimeter is $38\:in$ . What is the length of its shorter side?

Possible Answers:

$12\:in$

$5\:in$

$8\:in$

$14\:in$

$7\:in$

Correct answer:

$5\:in$

Explanation:

We know that the following two equations hold for rectangles. For area:

A=WL

For perimeter:

P=2W+2L

Now, for our data, we know:

70=WL

38=2W+2L

Now, solve the first equation for one of the variables:

$W=\frac{70}{L}$

Now, substitute this value into the second equation:

$38=2(\frac{70}{L})+2L$

Solve for :

$38=\frac{140}{L}+2L$

Multiply both sides by :

38L=140+2L^2

Solve as a quadratic. Divide through by :

19L=70+L^2

Now, get the equation into standard form:

L^2-19L+70=0

Factor this:

(L-14)(L-5)=0

This means that 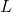(or ) would equal either $5\:in$ or $14\:in$ . Therefore, your answer is $5\:in$ .

Report an Error

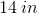
Example Question #1 : How To Find The Length Of The Diagonal Of A Rectangle

Given Rectangle ABCD.

Quantity A: The length of diagonal AC times the length of diagonal BD

Quantity B: The square of half of ABCD's perimeter

Possible Answers:

Quantity A is greater.

The relationship cannot be determined from the information given.

The two quantities are equal.

Quantity B is greater.

Correct answer:

Quantity B is greater.

Explanation:

Suppose ABCD has sides a and b.

The length of one of ABCD's diagonals is given by a²+ b² = c^2,where c is one of the diagonals.

Note that both diagonals are of the same length.

Quantity A: The length of diagonal AC times the length of diagonal BD

This is c * c = c^2.

Quantity A = c² = a²+ b²

Now for Quantity B, remember that the perimeter of a rectangle with sides a and b is Perimeter = 2(a + b).

Half of Perimeter = (a + b)

Square Half of Perimeter = (a + b)²

Use FOIL: (a + b)² = a²+ 2ab + b²

Quantity B = (a + b)² = a²+ 2ab + b²

The question is asking us to compare a²+ b² with a²+ 2ab + b^2.

Note that as long as a and b are positive numbers (in this case a and b are dimensions of a rectangle, so they must be positive), the second quantity will be greater.

Report an Error

Example Question #152 : Geometry

If rectangle ABCD has a perimeter of , and the longer edge is 2.4 times longer than the shorter edge, then how long is the diagonal ?

Possible Answers:

Correct answer:

Explanation:

Lets call our longer side L and our shorter side W.

If the perimeter is equal to 68, then

2L+2W=68 .

We also have that

L=2.4W .

If we then plug this into our equation for perimeter, we get 6.8W=68 .

Therefore, W=10 and L=24 . Using the Pythagorean Theorem, we have 10^2+24^2=676=D^2 so D=26 .

Report an Error

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GRE Tutors in San Diego, French Tutors in Dallas Fort Worth, SAT Tutors in Washington DC, French Tutors in New York City, SSAT Tutors in Seattle, ACT Tutors in Atlanta, GRE Tutors in Seattle, English Tutors in New York City, Spanish Tutors in Houston, ACT Tutors in Boston

Popular Courses & Classes

GRE Courses & Classes in Philadelphia, Spanish Courses & Classes in Chicago, ISEE Courses & Classes in Houston, GMAT Courses & Classes in Miami, SSAT Courses & Classes in Atlanta, ACT Courses & Classes in Houston, GMAT Courses & Classes in Seattle, SSAT Courses & Classes in Philadelphia, GMAT Courses & Classes in Los Angeles, Spanish Courses & Classes in Phoenix

Popular Test Prep

LSAT Test Prep in Philadelphia, ISEE Test Prep in San Diego, GMAT Test Prep in Chicago, LSAT Test Prep in Los Angeles, LSAT Test Prep in Seattle, GMAT Test Prep in Los Angeles, SSAT Test Prep in Chicago, SSAT Test Prep in San Francisco-Bay Area, LSAT Test Prep in San Francisco-Bay Area, SAT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

Email address:
Your name:
Feedback:

GRE Math : GRE Quantitative Reasoning

Study concepts, example questions & explanations for GRE Math

All GRE Math Resources

Example Questions

Example Question #1 : How To Find The Length Of The Side Of A Parallelogram

Example Question #1342 : Gre Quantitative Reasoning

Example Question #1343 : Gre Quantitative Reasoning

Example Question #25 : Quadrilaterals

Example Question #1341 : Gre Quantitative Reasoning

Example Question #151 : Plane Geometry

Example Question #31 : Quadrilaterals

Example Question #1 : Rectangles

Example Question #1 : How To Find The Length Of The Diagonal Of A Rectangle

Example Question #152 : Geometry

All GRE Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details