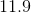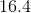This problem is dealing with the repeated trials for an event that only has two potential outcomes. This scenario describes a binomial distribution.

For  trials, each of which has a probability  of a 'successful' outcome, the probability of exactly  successes is given by the function:

Now, when there is language such as 'at least' or 'no more than', a cumulative probability can be assumed. I.e. we sum up the probabilities of each event that satisfies the condition. For example, if we're asked for the probability of rolling a three on a die at least two times out of four, we'd sum up the probability of rolling  a three twice, a three thrice, and a three four times. If we're asked for the probability rolling a three no more than once out of four times, we'd sum up the probabilities of rolling a three once, and of rolling a three zero times. 

The probability of rolling a sixteen or greater is . This can be seen by dividing the number of events that satisfy this by the number of total possible events: 

Now, to get this sixteen or greater at least twice out of three rolls:

The probability of Abel winning is

Looks like the odds favor the orc.

Consider first all of the possible ways the men may be arranged, which is

Now, consider all of the ways that Aaron and Gary could be seated beside each other; it may be easier to visualize by drawing it out:

1. A G _ _
2. G A _ _
3. _ A G _
4. _ G A _
5. _ _ A G
6. _ _ G A

As seen, there are six possibilities.

Finally, for each of these cases, Craige and Boone could be seated in one of two ways.

So the probability that Aaron and Gary will be seated beside each other is:

To solve this problem, employ the fundamentals of combinatorics. For the first digit of the number, you might think that there are 10 options (the digits 0-9), but remember that no seven-digit integer would start with 0 (e.g. you don't represent one-hundred thousand as 0,100,000). So there are 9 choices available for the first digit.

For the second digit, there are also 9 choices: 0 is now a possibility, but you cannot repeat the original digit.

For each remaining spot, you lose one option because you cannot match the unique digits you've already chosen.  For the third digit you have two of the ten options unavailable because you're chosen two already; for the fourth digit you cannot match the previous three, and so on.  So the calculation becomes:

9 * 9 * 8 * 7 * 6 * 5 * 4 = 544,320. 

This problem is dealing with binomial probabilities. For a probability of success, , and  trials, the probability of  successes is:

For this problem there are three trials, and we're interested in at least two successes. Note that this probability equation gives the probability of getting EXACTLY k succeeses, so we must consider getting three successes at well.

The probability of rolling at least a six on a twenty-sided die is 

Therefore, the probability of rolling this at least twice out of three trials is:

Answer: –1
Explanation: Recall that the median of an even-numbered set of numbers is the arithmetic mean of the pair of middle terms. Thus (4 + x)/2 = median of the first set and (5 + y)/2 = median of the second set. Since both medians are equal, we can set the equations equal to eachother. (4 + x)/2 = (5 + y)/2. Multiply both sides by 2 and we get 4 + x = 5 + y. We also know that 4 < x < 8 and 5 < y < 9, since the sets are arranged in ascending order. This narrows our options for x and y down significantly. Plugging in various values will eventually get you to x = 7 and y = 6, since 7 + 4 = 11 and 5 + 6 = 11, and thus the median in both cases would be 5.5. Thus, y – x = –1.

16, 19, 16, 7, 2, 20, 9, 5

Order the numbers from smallest to largest.

2,5,7,9,16,16,19,20

The median is the number in the middle.

In this case, there is a 9 and 16 in the middle.

When that happens, take the average of the two numbers.

To find the median, arrange the numbers from smallest to largest:

 4,4,4,4,6,7,9,9,12,12,12,12,12,12,18,76,90

There are 17 numbers in total.  Since 17 is an odd number, the median will be the middle number of the set.  In this case, it is the 9th number, which is 12.

Treat the percentages as a list, as we are including every demographic from the 3 vehicle types mentioned. If we do each 0.06(5000), 0.12(5000), and 0.15(5000) we note from observation that the median, or middle value, would have to be the 12% row since the sample size does not change. The question asks for EITHER of the 3 categories, so we can ignore the other two.

0.12(5000) = 600 (van) is the median of the 3 categories.

Begin by ordering the set from smallest to largest:

Already, we see that the mode is 8. Find the median by taking the average of the two middle numbers:

Find the mean by adding all numbers and dividing by the total number of terms:

Of the three, the mean of the set is the largest.

To solve this problem, we must be aware of the definition of a median for a set of numbers. The median is defined as the number that is in middle of a set of numbers sorted from smallest to largest. Therefore we must first sort the numbers from largest to smallest.

34,43,45,50,56,65,70,76,76,82,87,88,92,95,100

43,45,50,56,65,70,76,76,81,87,88,82,95

45,50,56,65,70,76,76,81,87,88,82

50,56,65,70,76,76,81,87,88

56,65,70,76,76,81,87

65,70,76,76,81

70,76,76

76

Then by slowly eliminating the smallest and the largest numbers we find that the median score for this test is 76.