All GRE Math Resources
Example Questions
Example Question #38 : How To Find Arithmetic Mean
What is the average grade of a student who got a 









In order to solve this problem, we must know how to find the arithmetic mean for a set of numbers. The arithmetic mean is defined as the sum of all the numbers added up divided by the number. In this case, we first have to find the amount of credits present. Adding all the credits up, we find there are 15 credits. Now, by adding up the grades for each of those credits and dividing by the total number of credits, we can solve for the average grade of the student.
Example Question #1 : How To Find Mode
Find the mode of the following set of numbers:
4,6,12,9,12,90,12,18,12,12,12,4,4,4,9,7,76
6
4
18
90
12
12
Mode is the item that appears most often.
Example Question #1 : Mode
Find the mode:
The mode is the number that appears most frequently in a given set.
Example Question #2 : Mode
The Bobcats scored 91, 83, 82, 82, 78, 87, 89, 96, and 86 points in their last nine home games. What is the difference between the average and the mode of their points scored?
Cannot be determined
The average is the sum of the points scored in the last nine games divided by 9, which equals 86. The mode is the score which occurs most often, 82. 86 – 82 = 4
Example Question #51 : Statistics
A survey has shown that the number of children that newlyweds plan to have is 
To solve this problem, we must be clear on the definition of the mode of a set of numbers. The mode is defined as the number that occurs the most frequently within a set of numbers. In this case, we can see that the number 1 occurs 3 times, the number 2 occurs 4 times, the number 3 occurs 3 times, the number 4 occurs 2 times and the number 5 occurs only one time. Therefore the mode of this survey is 2.
Example Question #4 : How To Find Mode
Quantity A: The mode of
Quantity B: The median of
The relationship cannot be determined.
Quantity A is greater.
Quantity B is greater.
The two quantities are equal.
The two quantities are equal.
Begin by organizing the set in numerical order
The mode is the value which repeats the most, so
Quantity A:
Now, since there are an even number of values, the median is the average of the two middle values:
Quantity B:
The two quantities are equal.
Example Question #3 : Mode
What is the mode of the following set of numbers?
The mode is the most occuring value in a set. 
Example Question #1 : How To Find Range
Quantitative Comparison
A set of numbers, Set A, has a mean of 4 and a standard deviation of 2. Another set, Set B, has a mean of 100 and a standard deviation of 20.
Quantity A: dispersion of numbers in Set A
Quantity B: dispersion of numbers in Set B
The two quantities are equal.
Quantity B is greater.
The relationship cannot be determined from the information given.
Quantity A is greater.
Quantity B is greater.
The standard deviation tells us how much variation, or dispersion, there is on average between the numbers in a set and their mean. Therefore Quantity B is greater, because Set B has a larger standard deviation than Set A.
Example Question #1 : Range
Find the range of the following set of numbers:
Cannot be determined.
The range is the difference between the largest and smallest numbers of a set. The biggest number is 15 and the smallest is 1, so our range is 15 – 1 = 14.
Example Question #2 : How To Find Range
Quantity A:
The sum of the median and mode of Set G
Quantity B:
The range of Set G
The relationship cannot be determined from the information given.
Quantity A is greater.
The two quantities are equal.
Quantity B is greater.
Quantity A is greater.
The median is the middle value in a set of numbers, and the mode is the number that occurs.
In Column A, the median is 6 and the mode is 6, so the sum of the median and the mode of Set G is 12.
The range is the difference between the highest and lowest numbers of the set.
In Column B, the range is 12 – 2 = 10.
Column A is greater than Column B.
All GRE Math Resources









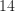
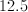
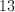










![Set_A=[1,4,10,1,3,4,10,4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/488970/gif.latex)


![Set_A=[1,4,10,1,3,4,10,4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/488971/gif.latex)
![Set_A=[1,1,3,4,4,4,10,10]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/488972/gif.latex)













![G= [2, 4, 5, 5, 6, 6, 6, 10, 12]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/179909/gif.latex)



