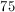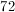All GRE Math Resources
Example Questions
Example Question #11 : Permutation / Combination
10 people want to sit on a bench, but the bench only has 4 seats. How many arrangements are possible?
4230
1020
1400
5040
6500
5040
The first seat can be filled in 10 ways, the second in 9 ways, the third in 8 ways, and the fourth in 7 ways. So the number of arrangements = 10 * 9 * 8 * 7 = 5040.
Example Question #322 : Arithmetic
There are 16 members of a club. 4 will be selected to leadership positions. How many combinations of leaders are possible?
2184
16
4
1820
43,680
1820
With permutations and combinations, you have to know if the order people are selected matters or not. If not, like in this case, you must take the number of people and positions available: 
Example Question #321 : Arithmetic
A restaurant serves its steak entree cooked rare, medium, or well done. The customer has the choice of salad or soup, with one of two salads or one of 4 soups. The customer also chooses between one of three soft drinks as well as water or milk. How many unique variations are there to the entire steak dinner of
steak + soup/salad + drink?
The customer has 3 choices on meat, 6 choices on side, and 5 choices on drink. This gives a total of 
Example Question #12 : Permutation / Combination
From a group of 8 students, 3 are attending a meeting.
Quantity A: The number of different groups that could attend among the 8 students
Quantity B: 336
The relationship cannot be determined from the information given.
The two quantities are equal.
Quantity B is greater.
Quantity A is greater.
Quantity B is greater.
To solve this problem, you would need to utilize the combination formula, which is 




336 would be the result of computing the permutation, which would be incorrect in this case.
Example Question #13 : Permutation / Combination
Michael owns 10 paintings. Michael would like to hang a single painting in each of five different rooms. How many different ways are there for Michael to hang 5 of his 10 paintings?
This problem involves the permutation of 10 items across 5 slots. The first slot (room) can have 10 different paintings, the second slot can have 9 (one is already in the first room), the third slot can have 8 and so on. The number of possibilities is obtained by multiplying the number of possible options in each of the 5 slots together, which here is 
Example Question #14 : Permutation / Combination
How many different committees of 3 people can be formed from a group of 7 people?
There are 


Example Question #15 : Permutation / Combination
A restaurant has a meal special that allows you to choose one of three salads, one of five sandwiches, and two of fifteen side dishes. How many possible combinations are there for the meal?
Although this is a permutation style problem, we have to be careful regarding the last portion (i.e. the side dishes). We know that our meal will have:
(3 possible salads) * (5 possible sandwiches) * (x possible combinations of side dishes).
We must ascertain how many side dishes can be selected. Now, it does not matter what order we put together the side dishes, so we have to use the combinations formula:
c(n,r) = (n!) / ((n-r)! * (r!))
Plugging in, we get: c(15,2) = 15! / (13! * 2!) = 15 * 14 / 2 = 15 * 7 = 105
Using this in the equation above, we get: 3 * 5 * 105 = 1575
Example Question #322 : Arithmetic
The President has to choose from six members of congress to serve on a committee of three possible members. How many different groups of three could he choose?
60
120
20
9
20
This is a combinations problem which means order does not matter. For his first choice the president can choose from 6, the second 5, and the third 4 so you may think the answer is 6 * 5 * 4, or 120; however this would be the answer if he were choosing an ordered set like vice president, secretary of state, and chief of staff. In this case order does not matter, so you must divide the 6 * 5 * 4 by 3 * 2 * 1, for the three seats he’s choosing. The answer is 120/6, or 20.
Example Question #22 : Permutation / Combination
Mohammed is being treated to ice cream for his birthday, and he's allowed to build a three-scoop sundae from any of the thirty-one available flavors, with the only condition being that each of these flavors be unique. He's also allowed to pick 

Knowing these details, how many sundae combinations are available?
Because order is not important in this problem (i.e. chocolate chip, pecan, butterscotch is no different than pecan, butterscotch, chocolate chip), it is dealing with combinations rather than permutations.
The formula for a combination is given as:
where 

For the ice cream choices, there are thirty-one options to build a three-scoop sundae. So, the number of ice cream combinations is given as:
Now, for the topping combinations, we are told there are ten options and that Mohammed is allowed to pick two items; however, we are also told that Mohammed has already chosen one, so this leaves nine options with one item being selected:
So there are 9 "combinations" (using the word a bit loosely) available for the toppings. This is perhaps intuitive, but it's worth doing the math.

Example Question #23 : Permutation / Combination
If there are 

To solve this problem, we must understand the concept of combination/permutations. A combination is used when the order doesn't matter while a permutation is used when order matters. In this problem, the two class representatives are randomly chosen, therefore it doesn't matter what order the representative is chosen in, the end result is the same. The general formula for combinations is 


Plugging in choosing 2 people from a group of 20, we find



All GRE Math Resources