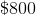All GRE Math Resources
Example Questions
Example Question #11 : How To Find The Percent Of Increase
In 2014, approximately of Americans were considered charming. In 2013 approximately 27.1% of Americans were deemed charming. If the population of America in 2013 was people and the population of America in 2014 was roughly people, what is the percent increase/decrease of charming people from 2013-2014? Round to the nearest tenth.
To solve this problem, we must understand that we can't simply use the percentage change from 2013-2014 in order to solve this problem. Because the populations change, simply using the percentage change in order to is invalid. Therefore we must find the amount of people that were charming in each year to solve for this problem.
In 2013, of the people in America were considered charming, this means that the number of charming people in America in 2013 is people.
In 2014, of the people in America were considered charming, this means that the number of charming people in America in 2014 is people.
Therefore to find the percent increase of charming people, we simply find the difference in charming people from 2013-2014 and divide by the number of charming people in 2013. or a increase in charming people.
Example Question #71 : Percentage
A new TV at some store goes on sale for off the retail price. A customer comes in to buy the TV, and in addition to the store discount of , uses a coupon for an extra off. The customer ends up paying of the original price of the TV. What is the original price of the TV?
Let represent the original price of the TV. Now, set up an equation where the discounted price of the TV (10% discount) minus 200 dollars is equal to 65% of the original price of the TV:
Solve for
The original price of the TV is .
Example Question #1 : How To Find The Sale Price
A winter shirt is regularly priced at $50. At the end of the Christmas season, it is marked down by 40%. A month after this initial markdown, it is marked back up by 50%.
Quantity A
The initial cost of the shirt.
Quantity B
The final cost of the shirt, after it is marked up.
Quantity A is greater.
The relationship cannot be determined from the information given.
Quantity B is greater.
The quantities are equal.
Quantity A is greater.
There are two ways to consider the value of B. First, you can subtract 40% from the initial $50 dollars: $50 – 0.4 * $50 = $30. This gives you the value after the markdown. Then to mark up the price, add 50% of $30 to the $30: $30 + 0.5 * $30 = $45.
A shorter way to do this problem is to consider the first markdown as reducing the price to 60% of the original, then considering the markup as making it 150% of the new price. This can be done in one set of multiplications: $50 * 0.6 * 1.5 = $45. Either way, the answer is the same. A is the larger quantity.
Example Question #71 : Percentage
A store puts a $200 dress on a 70% discount and then takes an additional 15% off the reduced price. How much of the original price was removed?
$30
$149
$170
$51
$161
$149
If we multiply $200 by 0.7, we find the dress has been reduced by $140 on the first discount. Since the dress now costs $60, we multiply that by 0.15 and find the dress has been discounted by an additional $9. The final sale of the dress is $51, with $149 of the original price removed.
Example Question #72 : Percentage
In a local store, pens that normally sell for 49 cents each are on sale at 3 for 99 cents. How much can be saved by purchasing 12 of these pens at the sale price?
$1.92
$2.00
$1.44
$3.00
$2.04
$1.92
Normally, 3 pens cost 3 * .49 = $1.47. Thus, on each set of 3 pens, the sale price saves the customer $1.47 - 99 = 48 cents. Multiply this by 4 to get the savings for 12 pens, and you get .48 * 4 = $1.92.
Example Question #1 : How To Find The Sale Price
A department store sells a set of hand weights for $X. If the store offers a 20% discount on the original price of the weights, and then an additional 10% employee discount, what will be the price of the weights if an employee purchases them?
0.8X
0.64X
0.7X
0.88X
0.72X
0.72X
This is a straightforward percentage problem. After the first discount, the price of the weights is $0.8X. This price is then further reduced by 10% for the employee discount. 90% of 0.8X = 0.9(0.8X) = 0.72X.
Example Question #73 : Percentage
A shirt is originally $20 and marked down 30%. After this it is marked up by 40% then marked down again by 10%. What is its final price?
$18.50
$17.64
$20
None of the other answers
$7.56
$17.64
The easiest way to solve this is to note that a 30% markdown reduces the cost to 70% of the original cost. Likewise, a 40% markup is the same as making the price 140% of its current value. Using this, we can solve our problem in one string of multiplications:
New cost = Original * 0.7 * 1.4 * 0.9
New cost = 20 * 0.7 * 1.4 * 0.9 = 17.64
Example Question #291 : Arithmetic
A dress originally costs $50 but is on sale for 25% off. In addition, you have a 10% off coupon. How much will the dress cost after these discounts?
$42.15
$33.75
$32.50
$35.25
$33.75
To find 25% of $50 you multiply 50 and 0.25. This gives you 12.50. This means the dress is $12.50 cheaper, so it now costs 50 – 12.50 = $37.50. You have an additional 10% off, so you multiply 37.50 by 0.10 to get 3.75. 37.50 – 3.75 = $33.75. This is the cost of the dress. NOTE: You CANNOT add 25% and 10% and take 35% off of the $50 dress. You will get the wrong answer.
Example Question #1 : Sale Prices
Product X costs $27 to manufacture at the rate of 50 per hour. Production can only be increased in groups of 10 units per hour. For each such increase, the production cost increases 30% of its previous amount. If the output is to be doubled, for how much must each unit be sold to make at least a 25% profit?
$219.38
$125.32
$213.75
$198.28
$157.32
$125.32
To calculate a 30% increase in cost, you can multiply the base cost by 1.3; therefore, if we are going to increase the rate five times, we will multiply by 1.3 five times, which is the same as 1.35. The cost of creating 100 units per hour is 27 * 1.35 = 100.25.
If we want to make a 25% profit, we can set up the equation:
Price = 1.25 * 100.25 or 125.3125. To make at least a 25%, this will be $125.32.
Example Question #6 : How To Find The Sale Price
To promote a new ice cream flavor, an ice cream parlor is selling their $1.29 cones at 70% of the original price. Approximately how much will be saved by buying 4 of their cones?
$1.29
$3.20
$1.56
$.90
$3.16
$1.56
First let's calculate what 70% of $1.29 is: .7(1.29) = .9
Next, calculate how much 4 cones would have cost at the original price vs. the sale price:
4(1.29) = 5.16
4(.9) = 3.60
5.16 – 3.60 = $1.56 saved
All GRE Math Resources