All GRE Math Resources
Example Questions
Example Question #301 : Arithmetic
Betty buys a sweater for $36. The next week, Alice buys the same sweater on sale for 25% off. The week after that, Chelsea buys the same sweater that is now 15% off the sale price. How much did Chelsea spend on the sweater?
$30
$30.60
$27
$22.95
$21.60
$22.95
The sweater price starts at $36. Alice pays $36 – (.25 * $36) = $27. Chelsea then pays $27 – (.15 * $27) = $22.95, which is the correct answer.
When solving percentage questions such as this one, do NOT try to add up the discounts and find the final sale price all in one step. If you tried to do that here, the answer would have been $36 – (.25 + .15) * $36 = $21.60. This is an answer choice, but the wrong answer! Most GRE percentage questions will always give you this as one of your answer choices to try and trick you!
Example Question #302 : Arithmetic
How much does a sweater cost that is 18% more than a $50 dress?
54
64
59
68
55
59
18% of the dress is .18 * 50 = $9. Then the sweater costs $50 + $9 = $59.
Example Question #303 : Arithmetic
Jenny is at a store and would like to buy a shirt. The shirt is labelled 

Based on the shirts label, Jenny should pay 



Example Question #81 : Percentage
A car dealer purchased a used truck, marked it up to make a 30% profit, then sold it at a 30% discount from the sticker price.
Quantity A: The amount that the dealer paid for the truck
Quantity B: The amount for which the dealer sold the truck
Quantity A is greater
The two quantities are equal
The relationship cannot be determined from the information given
Quantity B is greater
Quantity A is greater
Since no price is given, you can pick $100 as the starting point for the value of the truck. $100 marked up 30% is $130, and the 30% discount brings it to $91.
Example Question #304 : Arithmetic
A retail chain wishes to make at least a 

None of the answers are correct.
Let's begin by finding the absolute amount necessary for a 27% profit. Following that, we will adjust for the needs of having a whole number price. If the sale price is S, we can set up the following equation:
(S – 23)/23 = 0.27
S – 23 = 6.21
S = 29.21
The product must, however, be sold for at least $30 because it has to be an integer value.
Example Question #82 : Percentage
A car dealer sold two trucks for 
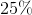

Quantity A: The dealer's net gain
Quantity B: The dealer's net loss
The two quantities are equal.
The relationship cannot be determined from the information given.
Quantity A is greater.
Quantity B is greater.
Quantity B is greater.
For the profitable truck, the dealer bought it for 


For the unprofitable truck, the dealer bought it for 


Thus, the dealer's net profit is $8,000, and the dealer's net loss is $10,000.
His loss is greater than his profit, so Quantity B is larger.
Example Question #83 : Percentage
The price of a laptop is reduced by 

Cannot be determined
To solve this problem, imagine that the original price of the laptop is $100. After the first 20% discount, the price of the laptop becomes $80. With the additional 10% reduction, we discount from $80, not $100. 10% of 80 is 8 so we must deduct $8 from $80. This gives $72 as the final price of the laptop after both reductions. Since we started at $100, the total discount is 28%.
Example Question #1 : How To Find Permutation Notation
A chamber of commerce board has seven total members, drawn from a pool of twenty candidates. There are two stages in the board's election process. First, a president, secretary, and treasurer are chosen. After that, four members are chosen to be “at large” without any specific title or district. How many possible boards could be chosen?
5,426,400
2,713,200
10,465,200
390,700,800
16,279,200
16,279,200
We have to consider two cases. First, the group containing the president, secretary, and treasurer represents a case of permutation. Since the order matters in such a group, we can select from our initial 20 candidates 20 * 19 * 18, or 6840 possible groupings.
Following that, the at large group constitutes a case of combinations in which the order does not matter. Since we have chosen 3 already for the first three slots, there will be 17 remaining people. The formula for choosing 4-person sets out of 17 candidates is represented by the combination formula of this form:
17! / ((17-4)! * 4!) = 17! / (13! * 4!) = (17 * 16 * 15 * 14) / (4 * 3 * 2) = 17 * 4 * 5 * 7 = 2380
Thus, we have 6840 and 2380 possible groupings. These can each be combined with each other, meaning that we have 6840 * 2380, or 16,279,200 potential boards.
Example Question #2 : How To Find Permutation Notation
How many ordered samples of 5 cards can be drawn from a deck of 52 cards without replacement?
65,690,040
42,365,000
311,875,200
500,320,000
11,452,000
311,875,200
The key points we need to remember are that order matters and that we are sampling without replacement. This then becomes a simple permutation problem. We have 52 cards to be chosen 5 at a time, so the answer is 52 * 51 * 50 * 49 * 48.
Example Question #1 : Permutation / Combination
Quantitative Comparison
3 cards are chosen from a standard 52-card deck.
Quantity A: The number of ways to choose 3 cards with replacement
Quantity B: The number of ways to choose 3 cards without replacement
The relationship cannot be determined from the information given.
Quantity B is greater.
The two quantities are equal.
Quantity A is greater.
Quantity A is greater.
Quantity A says with replacement, so we have 52 ways to choose the first card, then we replace it so we again have 52 ways to choose the 2nd card, and similarly we have 52 ways to choose the 3rd card. Therefore we have 52 * 52 * 52 ways of choosing 3 cards with replacement.
Quantity B says without replacement, so we have 52 ways to choose the first card, but then we don't put that card back in the deck so we have 51 ways to choose the second card. Again we don't put that card back, leaving 50 ways to choose the third card. Thus there are 52 * 51 * 50 ways of choosing 3 cards without replacement.
Clearly Quantity A is greater. In general, there should always be more ways to choose something with replacement than there are without replacement just as we showed above. If you already knew this, you could have picked Quantity A without the math. Notice that either way you come to the answer here, there is NO reason to finish the computations all the way through. This will save you time on many quantitative comparison problems. For example, we know that 52 * 52 * 52 is larger than 52 * 51 * 50 without actually figuring out what the two expressions equal.
All GRE Math Resources

















