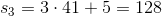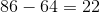Do not try to count out the factors. A neat formula for finding the sum of factors of a number can be utilized by first determining the prime factorization of the number.

, 

where s is the sum, a, b, and c are factors, and x, y, and z are the powers of these factors.

Then, a = 2, b = 5, x = 2, y = 2.

Then, a = 2, b = 5, x = 3, y = 2.

Now we can add our two sums.

This question is really asking, “How many factors of 4 are there in 16!”?  To ascertain this, list all the even numbers and count the total number of 2s among those factors.

Respectively, 16, 14, 12, 10, 8, 6, 4, 2 have 4, 1, 2, 1, 3, 1, 2, 1 factors of 2. 

The total then is 15. This means that you have a factor of 2¹⁵, which is the same as 4⁷ * 2; therefore, since you are asked for the largest integer value of n, 7 is your answer.

Any larger integer value would not allow 4ⁿ to divide 16! evenly.

Since we're dealing with a product that comes out to a positive value, it could be the product of two positives or two negatives.

That being said, consider the ways we could factor :

For each of these four possible factors, there are four possible sums:

When the product of two numbers is positive, that means that either both numbers were positive, or both numbers were negative.

Now, considering the way  could be factored:

And of course the cases where both values are negative. For each of these potential factors, the sums are then

Absolute value signs are used to denote that either a sum or it's negative suffices. However, recall that we're told the two integers are distinct!

Due to this, neither  or  is an acceptable answers, because both the integers would be equivalent and not distinct.

Since  is negative, it is the product of a positive and negative integer. Consider all of the ways that it could be factored, and the sums these factors would produce:

 is the answer choice that matches.

Prime numbers are numbers that can only divided by one and themselves.  Breaking 60 into its prime factors yields:

Do NOT try to add all of these.  It is key that you notice the pattern.  Begin by looking at the first and the last elements: 1 and 99.  They add up to 100.  Now, consider 3 and 97.  Just as 1 + 99 = 100, 3 + 97 = 100.  This holds true for the entire list.  Therefore, it is crucial that we find the number of such pairings.

1, 3, 5, 7, and 9 are paired with 99, 97, 95, 93, and 91, respectively.  Therefore, for each 10s digit, there are 5 pairings, or a total of 500.  To get all the way through our numbers, you will have to repeat this process for the 10s, 20s, 30s, and 40s (all the way to 49 + 51 = 100).

Therefore, there are 500 (per pairing) * 5 pairings = 2500.

With series, you can always "walk through" the values to find your answer. Based on our equation, we can rewrite  as :

You then continue for the third and the fourth element:

When you are asked to find elements in a series that are far into its iteration, you need to find the pattern. You absolutely cannot waste your time trying to calculate all of the values between  and . Notice that for every element after the first one, you subtract . Thus, for the second element you have:

For the third, you have:

Therefore, for the 40th and 70th elements, you will have:

The sum of these two elements is:

The first term and second term average out to 6. So the third term is 6. Now add 6 to the preceding two terms and divide by 3 to get the average of the first three terms, which is the value of the 4th term. This, too, is 6 (18/3)—all terms after the 2nd are 6, including the 39th. Thus, the answer is 6.