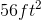To get rid of the radical, multiply top and bottom by .

Square both sides.

 is "opposite over adjacent," or . (This is because .)

Let's substitute  into the equation for  and multiply the numerator and the denominator by .

Now we can multiply the result by : 

 is the inverse of , or :

We can reduce the resulting  to : 

By multiplying top and bottom by , we can cancel out the  in the numerator:

The resulting fraction can be simplified:

To get rid of the radical, we need to multiply by the conjugate. The conjugate uses the opposite sign and multiplying by it will let us rationalize the denominator in this problem. The goal is getting an expression of  in which we are taking the differences of two squares.

You can "break apart" the fractional square root:

into:

Therefore, you can rewrite your equation as:

Now, multiply both sides by :

Now, you can square both sides of your equation and get:

The area of a square is length squared. In this case, that would be  which is equivalent to . At this point, you multiply the values underneath the square root, then simplify:

 .

The square root of a base squared is then just the base: 

Lastly, we apply the appropriate units, therefore the area of the courtyard is .

Begin by multiplying what is under the square roots together. Remember:

Therefore:

We must now try to reduce the square root. Look for factors that can be taken out that can be easily square-rooted. It's a good idea to start with small square roots . In this case, we can factor out a 9 from 135:

Now take the square root of 9, and we are left with our answer:

To solve this problem, we must know how to multiply/divide with square roots. The rules involved are quite simple. When multiplying square roots together, multiply the coeffcients of the two numbers together and then multiply the two radicands together. The product of the radicand becomes the new radicand and the product of the coeffcients become the new coeffcient. The radicand is simply the number within the square root.

Dividing square roots follows the exact same rules as multiplying square roots, divide the coeffcients together, the result is the coeffcient for final answer. Do the same for the radicands.

Begin by breaking down each of the roots in question.  Often, for the GRE, your answer arises out of doing such basic "simplification moves".

Quantity A

This is the same as:

, which can be reduced to:

Quantity B

This is the same as:

, which can be reduced to:

Now, since we know that  must be greater than , we know that .  Therefore, quantity A is larger.

Begin by subtracting  from both sides:

This simplifies to:

Now, while you could square both sides, you also know that  merely needs to be the same as the value under the other radical. This means that it is —simply and quickly! (Always work to save time on the exam!)

As always for comparison questions, work on getting your quantities explicit. In order to do this in this case, you must factor the roots.

Quantity A

This can be factored into:

Quantity B

This can be factored into:

This makes the comparison very easy! Since  is a larger number than , we know that  is a smaller value than . Therefore, Quantity B is larger.