GED Math : GED Math
Study concepts, example questions & explanations for GED Math
All GED Math Resources
Example Questions
Example Question #21 : Pie Charts
The following graph shows the distribution of students at a high school that has a student population of 
How many freshmen does this school have?
From the chart, we can see that 
Example Question #22 : Pie Charts
The following graph shows the distribution of students in a high school that has a student population of 
In degrees, what is the central angle of the sector labeled "Juniors"? Round to the nearest tenths place.
The sector labeled "Juniors" takes up 
The central angle must be 
Example Question #23 : Pie Charts
The following graph shows the distribution of students in a high school that has a student population of 
How many more juniors and seniors are there than freshmen and sophomores?
The juniors and seniors make up 
The freshmen and sophomores make up 
Subtract these two numbers to find how many more juniors and seniors there are than freshmen and sophomores.
There are 
Example Question #2071 : Ged Math
A school district includes five high schools - Burr, Colfax, Garner, Gerry, and Wallace. Seniors at all five high schools took the California state high school exit examination this year - the results are reflected in the above bar graph.
Which of the following questions cannot be answered about the math scores of the five schools by examining the above graph?
Of the five schools, which school's median math score was the lowest this year?
Of the five schools, which school's median score improved the most from last year?
Of the five schools, how many had median math scores above 70 this year?
What was the difference this year between the median math score of the highest-performing school of the five and that of the lowest-performing school?
Of the five schools, which school's median score improved the most from last year?
The question "Of the five schools, which school's median score improved the most from last year?" requires knowledge of last year's median math scores, which are not given by the graph. The other three questions only require knowledge of this year's scores, which are given.
Example Question #2072 : Ged Math
Refer to the above bar graph. The exit examination was given to all high school seniors in the above five schools.
Juanita attended Wallace High School and scored a 75 on the math portion. Wallace High School had 188 seniors take the examination. How many seniors could Juanitia have conceivably outscored?
The median score at Wallace was 69, so Juanita scored above the median. By definition, she outscored at least half the seniors, which means that she must have outscored at least 
Example Question #2073 : Ged Math
Refer to the above bar graph.
Three cousins took this examination this year- Carlos scored 67, Alberto scored 70, and Julio scored 71. All three attended the same high school and all three scored below the median for their school. Which of the following high schools could they have attended?
Gerry
Burr
Wallace
Garner
Garner
Julio scored the highest of the three with 71, so we are looking for a high school whose median score was above 71. Of the four choices, only Garner fits this criterion.
Example Question #2074 : Ged Math
The above bar graph compares the median math scores from both 2012 and 2013 for an examination administered in the five high schools of a school district.
How many of the five schools did not see their median math score reach at least 70 in either 2012 or 2013?
Two
One
None
Three
One
Of the five schools, only Burr had median scores below 70 in both 2012 and 2013. The correct choice is "one".
Example Question #2075 : Ged Math
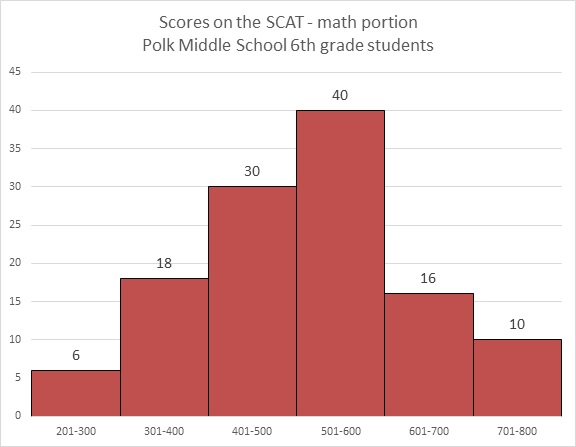
Refer to the above bar graph.
How many students at Polk Middle School scored higher than 600 on the math portion of the SCAT?
The number of students who scored in the 601-700 range is 16; in the 701-800 range, 10. Add them to get 26 students total.
Example Question #2076 : Ged Math
Refer to the above bar graph.
What percent of the students achieved a score above 500?
40 students achieved a score of 501-600; 16 achieved a score of 601-700; 10 achieved a score of 701-800. Add these:
The number of students who took the test is the sum of the students who finished in the six ranges:
The question is now to find out what percent 66 is of 120, which can be calculated as follows:
Example Question #2077 : Ged Math
Refer to the above graph. Clarissa, a sixth grader at Polk, scored a 673 on the math portion of the SCAT. Which of the following could have been her rank among the students?
By making a 673, Clarissa finished in the second-highest range shown (601-700). She was outscored by at least 10 students (the ones in the 701-800 range), but by at most 25 students (the 10 in the 701-800 range plus the other 15 in the 601-700 range). She finished between 11th and 26th, inclusive, so the only plausible choice is 14th.
All GED Math Resources
