Figuring out the perimeter of a square from this information is luckily pretty easy. Since the sides of a square are all the same size, you know also that .

Taking the square root of both sides, you get:

Now, the perimeter of the square is just , or .

Since the four sides of a square are equal, you know that the perimeter of a square is defined as:

For our data, this is:

Solving for , you get:

Now, the area of a square is just:

 or , which is the same as .

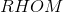
The figure referenced is below.

The sides of a rhombus are congruent by definition, so , making  isosceles (and possibly equilateral).

Also, consecutive angles of a rhombus are supplementary, as they are with all parallelograms, so

.

, having measure greater than , is obtuse, making  an obtuse triangle. Also, the triangle is not equilateral, since such a triangle must have three  angles.

The correct response is that  is obtuse and isosceles, but not equilateral.

Statement I asserts that two pairs of consecutive angles are congruent. This does not prove that the figure is a parallelogram. For example, an isosceles trapezoid has two pairs of congruent base angles, which are consecutive. 

Statement II asserts that both pairs of opposite angles are congruent. By a theorem of geometry, this proves the quadrilateral to be a parallelogram.

Statement III asserts that two pairs of consecutive angles are supplementary. While all parallelograms have this characteristic, trapezoids do as well, so this does not prove the figure a parallelogram.

The correct response is Statement II only.

A rectangle is defined as a parallelogram with four right, or , angles.

Since opposite angles of a paralellogram are congruent, if one angle measures , so does its opposite. Since consecutive angles of a paralellogram are supplementary - that is, their degree measures total  - if one angle measures , then both of the neighboring angles measure .

In short, in a parallelogram, if one angle is right, all are right and the parallelogram is a rectangle. All three statements assert that one angle is right, so from any one, it follows that the figure is a rectangle. The correct response is Statements I, II, or III.

Note that the sidelengths are irrelevant.

Write the area for a rectangle.

Substitute the given dimensions.

The answer is:  

Recall that in a quadrilateral, the interior angles must add up to .

Thus, we can solve for :

Now, to find the largest angle, plug in the value of  into each expression for each angle.

The largest angle is .

A polygon with eight sides is called an octagon.

In naming a polygon, the vertices must be written in the order in which they are positioned, going either clockwise or counterclockwise. Of the four choices, only Polygon  violates this convention, since  and  are not adjacent vertices (nor are  and ).

The figure can be viewed as the composite of rectangles. As such, we can take advantage of the fact that opposite sides of a rectangle have the same length, as follows:

Now that the missing sidelengths are known, we can add the sidelengths to find the perimeter: