We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

GED Math : Triangles

Study concepts, example questions & explanations for GED Math

Create An Account

All GED Math Resources

4 Diagnostic Tests 263 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 3 4 5 6 7 8 9 10 11 12 Next →

Example Question #2 : Similar Triangles And Proportions

Which of the following statements follows from the statement $\Delta KLM \sim \Delta XYZ$ ?

Possible Answers:

$\overline{KM} \cong \overline{XZ}$

$\angle K \cong \angle Y$

$\angle L \cong \angle M$

$\frac{KL}{LM } = \frac{XY}{YZ}$

Correct answer:

$\frac{KL}{LM } = \frac{XY}{YZ}$

Explanation:

The similarity of two triangles implies nothing about the relationship of two angles of the same triangle. Therefore, $\angle L \cong \angle M$ can be eliminated.

The similarity of two triangles implies that corresponding angles between the triangles are congruent. However, because of the positions of the letters, $\angle K$ in $\Delta KLM$ corresponds to $\angle X$ , not $\angle Y$ , in $\Delta XYZ$ , so $\angle K \cong \angle X$ . The statement $\angle K \cong \angle Y$ can be eliminated.

Similarity of two triangles does not imply any congruence between sides of the triangles, so $\overline{KM} \cong \overline{XZ}$ can be eliminated.

Similarity of triangles implies that corresponding sides are in proportion. $\overline{KL}$ and $\overline{LM}$ in $\Delta KLM$ correspond, respectively, to $\overline{XY}$ and $\overline{YZ}$ in $\Delta XYZ$ . Therefore, it follows that $\frac{KL}{LM } = \frac{XY}{YZ}$ , and this statement is the correct choice.

Report an Error

Example Question #3 : Similar Triangles And Proportions

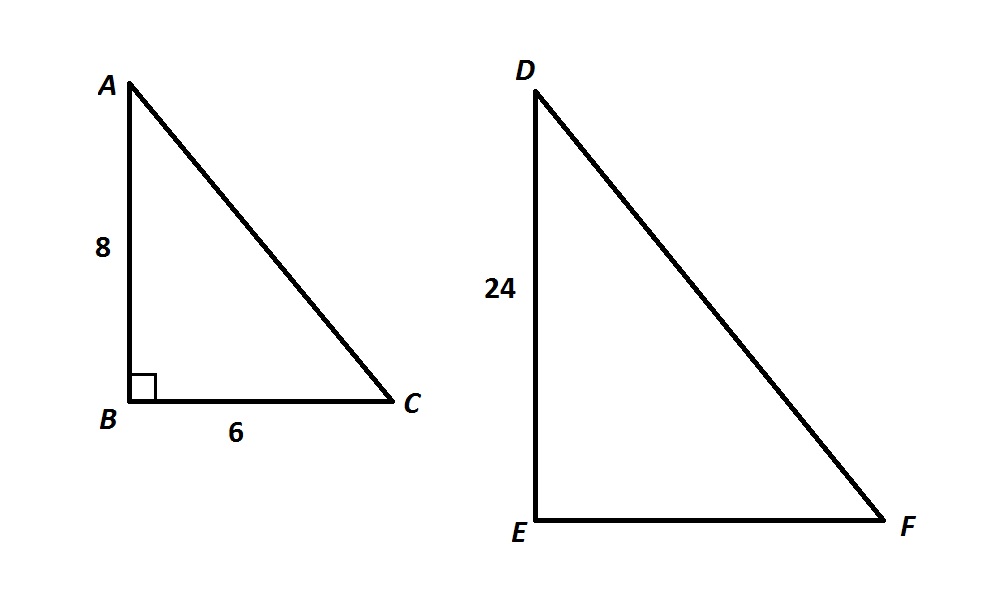
Triangles

Note: Figure NOT drawn to scale.

Refer to the above diagram. If $\Delta ABC \sim \Delta DE F$ , which of the following is false?

Possible Answers:

$\angle A \cong \angle D$

EF = 20

DF = 30

$\angle E$ is a right angle

Correct answer:

EF = 20

Explanation:

Suppose $\Delta ABC \sim \Delta DE F$ .

Corresponding angles of similar triangles are congruent, so $\angle A \cong \angle D$ . Also, $\angle B \cong \angle E$ , so, since $\angle B$ is a right angle, so is $\angle E$ .

Corresponding sides of similar triangles are in proportion. Since

$\frac{DE}{AB} = \frac{24}{8} = 3$ ,

the similarity ratio of $\Delta DE F$ to $\Delta ABC$ is 3.

By the Pythagorean Theorem, since is the hypotenuse of a right triangle with legs 6 and 8, its measure is

$AC = \sqrt{6^{2} + 8 ^{2}} = \sqrt{36 + 64 } = \sqrt{100} = 10$ .

$DF = 3 (AC) = 3 \cdot 10 = 30$ , so DF = 30 is a true statement.

But $EF = 3 (BC) = 3 \cdot 8 = 24 \neq 20$ , so EF = 20 is false if the triangles are similar. This is the correct choice.

Report an Error

Example Question #4 : Similar Triangles And Proportions

Triangles

Note: Figures NOT drawn to scale.

Refer to the above figures. Given that $\Delta ABC \sim \Delta DE F$ , evaluate .

Possible Answers:

$93\frac{1}{3}$

$52 \frac{1}{2}$

Correct answer:

Explanation:

By the Pythagorean Theorem, since is the hypotenuse of a right triangle with legs 6 and 8, its measure is

$AC = \sqrt{6^{2} + 8 ^{2}} = \sqrt{36 + 64 } = \sqrt{100} = 10$ .

The similarity ratio of $\Delta DE F$ to $\Delta ABC$ is

$\frac{DF}{AC} = \frac{70}{10} = 7$ .

Likewise,

$\frac{EF}{BC} = 7$

$\frac{EF}{6} = 7$

EF = 42

Report an Error

Example Question #5 : Similar Triangles And Proportions

Triangles

Note: Figures NOT drawn to scale.

Refer to the above figures. Given that $\Delta ABC \sim \Delta DE F$ , give the area of $\Delta DE F$ .

Possible Answers:

810

607.5

405

486

Correct answer:

486

Explanation:

Corresponding angles of similar triangles are congruent, so, since $\angle B$ is right, so is $\angle E$ . This makes $\overline{DE}$ and $\overline{EF}$ the legs of a right triangle, so its area is half their product.

By the Pythagorean Theorem, since is the hypotenuse of a right triangle with legs 6 and 8, its measure is

$AC = \sqrt{6^{2} + 8 ^{2}} = \sqrt{36 + 64 } = \sqrt{100} = 10$ .

The similarity ratio of $\Delta DE F$ to $\Delta ABC$ is

$\frac{DF}{AC} = \frac{45}{10} = 4.5$ .

This can be used to find and :

$\frac{DE}{AB} = 4.5$

$\frac{DE}{8} = 4.5$

$DE = 8 \cdot 4.5 = 36$

$\frac{EF}{BC} = 4.5$

$\frac{EF}{6} = 4.5$

$EF = 6 \cdot 4.5 = 27$

The area of $\Delta DE F$ is therefore

$\frac{1}{2} \cdot DE \cdot EF = \frac{1}{2} \cdot 36 \cdot 27 =486$ .

Report an Error

Example Question #6 : Similar Triangles And Proportions

In the figure below, the two triangles are similar. Find the value of .

Possible Answers:

Correct answer:

Explanation:

Since the two triangles are similar, we know that their corresponding sides must be in the same ratio to each other. Thus, we can write the following equation:

$\frac{12}{8}=\frac{9}{x}$

Now, solve for .

12x=72

x=6

Report an Error

Example Question #1 : Pythagorean Theorem

The two legs of a right triangle measure 30 and 40. What is its perimeter?

Possible Answers:

140

130

125

120

135

Correct answer:

120

Explanation:

By the Pythagorean Theorem, if a ,b are the legs of a right triangle and is its hypotenuse,

$c^{2} = a^{2} + b^{2}$

Substitute a = 30, b= 40 and solve for :

$c^{2} = 30 ^{2} + 40^{2} = 900 + 1,600 = 2,500$

$c = \sqrt{2,500} = 50$

The perimeter of the triangle is

P = 30 + 40 + 50 = 120

Report an Error

Example Question #2 : Pythagorean Theorem

A right triangle has legs 30 and 40. Give its perimeter.

Possible Answers:

120

1,200

600

Correct answer:

120

Explanation:

The hypotenuse of the right triangle can be calculated using the Pythagorean theorem:

$c = \sqrt{30^{2}+40^{2}} = \sqrt{900+1600} = \sqrt{2,500} = 50$

Add the three sides:

P = 30 + 40 + 50 = 120

Report an Error

Example Question #3 : Pythagorean Theorem

A right triangle has one leg measuring 14 inches; its hypotenuse is 50 inches. Give its perimeter.

Possible Answers:

$64\textrm{ in}$

$114\textrm{ in}$

$112 \textrm{ in}$

$78 \textrm{ in}$

Correct answer:

$112 \textrm{ in}$

Explanation:

The Pythagorean Theorem can be used to derive the length of the second leg:

$b = \sqrt{50^{2}-14^{2}} = \sqrt{2,500 - 196} = \sqrt{2,304} = 48$ inches

Add the three sides to get the perimeter.

P = 14 + 48 + 50 = 112 inches.

Report an Error

Example Question #4 : Pythagorean Theorem

Whicih of the following could be the lengths of the sides of a right triangle?

Possible Answers:

10 inches, 1 foot, 14 inches

15 inches, 3 feet, 40 inches

2 feet, 32 inches, 40 inches

7 inches, 2 feet, 30 inches

Correct answer:

2 feet, 32 inches, 40 inches

Explanation:

A triangle is right if and only if it satisfies the Pythagorean relationship

$a ^{2}+ b^{2}= c^{2}$

where is the measure of the longest side and a,b are the other two sidelengths. We test each of the four sets of lengths, remembering to convert feet to inches by multiplying by 12.

7 inches, 2 feet, 30 inches:

2 feet is equal to 24 inches. The relationship to be tested is

$7^{2}+ 24 ^{2} = 30^{2}$

49 + 576 = 900

625 = 900 - False

10 inches, 1 foot, 14 inches:

1 foot is equal to 12 inches. The relationship to be tested is

$10^{2}+ 12^{2}= 14^{2}$

100 + 144 = 196

244 = 196 - False

15 inches, 3 feet, 40 inches:

3 feet is equal to 36 inches. The relationship to be tested is

$15^{2}+ 36^{2} = 40^{2}$

225 + 1,296 = 1,600

1,521 = 1,600 - False

2 feet, 32 inches, 40 inches:

2 feet is equal to 24 inches. The relationship to be tested is

$24 ^{2}+ 32^{2} = 40^{2}$

576+ 1,024= 1,600

1,600 =1,600 - True

The correct choice is 2 feet, 32 inches, 40 inches.

Report an Error

Example Question #5 : Pythagorean Theorem

An isosceles right triangle has hypotenuse 80 inches. Give its perimeter. (If not exact, round to the nearest tenth of an inch.)

Possible Answers:

$153.1 \textrm{ in}$

$193.1 \textrm{ in}$

$96.6\textrm{ in}$

$136.6\textrm{ in}$

Correct answer:

$193.1 \textrm{ in}$

Explanation:

Each leg of an isosceles right triangle has length that is the length of the hypotenuse divided by $\sqrt{2}$ . The hypotenuse has length 80, so each leg has length

$\frac{80}{\sqrt{2}} = \frac{80\cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}}= \frac{80 \sqrt{2}}{2} = 40 \sqrt{2}$ .

The perimeter is the sum of the three sides:

$80 + 40 \sqrt{2}+ 40\sqrt{2}= 80 + 80\sqrt{2}$ inches.To the nearest tenth:

$80 + 80\sqrt{2} \approx 80 + 80 \times 1.414 \approx 80 + 113.1 = 193.1$ inches.

Report an Error

← Previous 1 2 3 4 5 6 7 8 9 10 11 12 Next →

View Tutors

Maria Angelica
Certified Tutor

Universidad Pedagógica Nacional, Bachelor of Education, Foreign Language Teacher Education. Universidad de los Andes, Master ...

View Tutors

Ravi
Certified Tutor

Indian Institute of Technology - Mumbai, Bachelor of Technology, Mechanical Engineering. University of Cincinnati-Main Campus...

View Tutors

Erik
Certified Tutor

University of Illinois at Urbana-Champaign, Bachelor of Science, Physics. University of California-San Diego, Master of Scien...

All GED Math Resources

4 Diagnostic Tests 263 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Houston, ACT Tutors in Denver, SSAT Tutors in Houston, Calculus Tutors in Washington DC, ISEE Tutors in Denver, GMAT Tutors in Washington DC, Biology Tutors in Boston, ACT Tutors in Washington DC, Algebra Tutors in Miami, Computer Science Tutors in Los Angeles

Popular Courses & Classes

GMAT Courses & Classes in Washington DC, SSAT Courses & Classes in Chicago, GRE Courses & Classes in Chicago, ACT Courses & Classes in Chicago, ACT Courses & Classes in Atlanta, ACT Courses & Classes in Miami, SAT Courses & Classes in Washington DC, MCAT Courses & Classes in Philadelphia, GRE Courses & Classes in Houston, GMAT Courses & Classes in Los Angeles

Popular Test Prep

ACT Test Prep in Chicago, SAT Test Prep in Los Angeles, ISEE Test Prep in Dallas Fort Worth, LSAT Test Prep in Philadelphia, MCAT Test Prep in Philadelphia, ACT Test Prep in Atlanta, SAT Test Prep in Denver, SSAT Test Prep in Boston, LSAT Test Prep in Denver, SSAT Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

GED Math : Triangles

Study concepts, example questions & explanations for GED Math

All GED Math Resources

Example Questions

Example Question #2 : Similar Triangles And Proportions

Example Question #3 : Similar Triangles And Proportions

Example Question #4 : Similar Triangles And Proportions

Example Question #5 : Similar Triangles And Proportions

Example Question #6 : Similar Triangles And Proportions

Example Question #1 : Pythagorean Theorem

Example Question #2 : Pythagorean Theorem

Example Question #3 : Pythagorean Theorem

Example Question #4 : Pythagorean Theorem

Example Question #5 : Pythagorean Theorem

All GED Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: