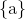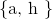All Finite Mathematics Resources
Example Questions
Example Question #61 : Finite Mathematics
Consider the conditional statements:
"If Mickey is a Freemason, then Nelson is a Freemason."
"If Oscar is not a Freemason, then Nelson is not a Freemason."
Nelson is a Freemason. What can be concluded about whether or not Mickey and Oscar are Freemasons?
Mickey and Oscar are both Freemasons.
Mickey is a Freemason; no conclusion can be drawn about Oscar.
Mickey is a Freemason; Oscar is not a Freemason.
Oscar is a Freemason; no conclusion can be drawn about Mickey.
No conclusion can be drawn about either Mickey or Oscar.
Oscar is a Freemason; no conclusion can be drawn about Mickey.
Consider the second conditional "If Oscar is not a Freemason, then Nelson is not a Freemason.". It is known that Nelson is a Freemason, making the consequent of this conditional false. By a modus tollens argument, it follows that the antecedent is also false, and Oscar is a Freemason.
No conclusion can be drawn about Mickey, however. If Mickey is a Freemason, then by the first conditional, it follows that Nelson is a Freemason, which is already known; if Mickey is not a Freemason, no conclusion can be drawn that is inconsistent with what is known. Thus, either status is consistent with Nelson and Oscar both being Freemasons.
Example Question #62 : Finite Mathematics
Let 

True or false: 
False
True
True
A set is well-defined if each element can be identified with certainty as being or not being an element of the set. Since, for any value of 

Example Question #23 : Logic, Sets, And Counting
The state of A has passed a law stating that all license plate numbers must adhere to the following rules:
1) There must be seven characters, each a numeral or a letter.
2) The first character may be a numeral or a letter, but either way, letters and numerals must alternate.
3) Repetition is allowed.
How many license plate numbers are possible under these rules?
Let L stand for a letter and N stand for a numeral. One of two events will happen - the selection of a license plate with the pattern LNLNLNL, or the selection of a license plate with pattern NLNLNLN. These events are mutually exclusive, so we can count the number of ways to obtain them separately, then add.
There are no restrictions as to which letters or numerals can be chosen, or how many times each can be chosen, so the number of ways to choose a license plate number with the pattern LNLNLNL is

The number of ways to choose a license plate number with the pattern NLNLNLN is

Add these to get

the total number of license plates possible.
Example Question #63 : Finite Mathematics
Consider the conditional statement
If 

Give the inverse of this statement.
If 

If 

If 

If 

If 

If 

Call 





The inverse of this conditional is the conditional "If (not 

"Not 





Thus, the inverse of the conditional is
"If 

Example Question #63 : Finite Mathematics
Consider the statements:


True or false: 

False
True
False
The negation of a statement 




Example Question #65 : Finite Mathematics
Define the universal set 
Let 

Which of the following is equal to the set 




It follows that

Example Question #66 : Finite Mathematics
Define the universal set 
Let 

Which of the following is equal to the set 







The union, including duplicates, is
Arrange, and eliminate the duplicates, shown in red:
Example Question #27 : Logic, Sets, And Counting
Consider the statement
"If 

Which is true - its converse or its inverse?
Both the converse and the inverse are true.
Both the converse and the inverse are false.
The converse is false, but the inverse is true.
The converse is true, but the inverse is false.
Both the converse and the inverse are true.
The converse of a conditional statement reverses the antecedent and the consequent; the inverse negates both. That is, for a conditional
If 

the converse of the statement is
"If 

and the inverse is
"If (not 

This problem becomes easier if you know that the converse and the inverse of any conditional are logically equivalent - that is, one is true if and only the other is. It suffices to determine the truth value of one of them. The converse of the given conditional is the statement
"If 

This is easily proved true; if 


Example Question #21 : Logic, Sets, And Counting
Consider the logical proposition
"
True or false: The logical proposition "
True
False
True
The negation of a logical proposition 


The negation of the proposition "
![x \in (-\infty, 2] \cup [4, \infty )](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1047438/gif.latex)
![x \in (-\infty, 2] \cup [4, \infty )](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1047439/gif.latex)
![x \in (-\infty, 2] \cup [4, \infty )](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1047440/gif.latex)

Example Question #24 : Logic, Sets, And Counting
Define the universal set
Define 
How many proper subsets does 




A set with 





proper subsets.
All Finite Mathematics Resources