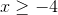We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Finite Mathematics : Finite Mathematics

Study concepts, example questions & explanations for Finite Mathematics

Create An Account

All Finite Mathematics Resources

1 Diagnostic Test 22 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 3 4 5 6 7 8 9 10 11 Next →

Example Question #1 : Solve A System Of Equations In Three Variables Using Augmented Matrices

$A = \begin{bmatrix} 0.7 & -0.4 \\ -0.8 & 0.2 \end{bmatrix}$ and $B= \begin{bmatrix} 0. 3 & 0.4 \\ 0.8 & 0.8 \end{bmatrix}$ .

True or false: A+ B = I , where is the two-by-two identity matrix.

Possible Answers:

False

True

Correct answer:

True

Explanation:

First, it must be established that A+ B is defined. This is the case if and only and have the same number of rows, which is true, and they have the same number of columns, which is also true. A +B is therefore defined.

Addition of two matrices is performed by adding corresponding elements, so

$A +B= \begin{bmatrix} 0.7 & -0.4 \\ -0.8 & 0.2 \end{bmatrix}+ \begin{bmatrix} 0. 3 & 0.4 \\ 0.8 & 0.8 \end{bmatrix}$

$= \begin{bmatrix} 0.7+0.3 & -0.4+0.4 \\ -0.8+0.8 & 0.2+0.8 \end{bmatrix}$

$= \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}$

This is the two-by-two identity . Therefore, A+ B = I .

Report an Error

Example Question #31 : Finite Mathematics

You are given that the inverse of the matrix

$A = \begin{bmatrix} 1 & -2 & 3 \\ -2 & 3 & 1 \\ -1 & 1 & 3 \end{bmatrix}$

$A^{-1} = \begin{bmatrix} 8 &9 & -11 \\ 5 & 6 & -7 \\ 1 & 1 & -1 \end{bmatrix}$

Using this information, solve the linear system

x-2y + 3z = 24

-2x+ 3y + z = 40

-x+ y+ 3z = -10

From these five choices, select the correct value of .

Possible Answers:

640

430

160

662

Correct answer:

430

Explanation:

The given linear system can be rewritten as the matrix equation

AX = B ,

where

$A = \begin{bmatrix} 1 & -2 & 3 \\ -2 & 3 & 1 \\ -1 & 1 & 3 \end{bmatrix}$ , $X= \begin{bmatrix} x \\ y \\ z \end{bmatrix}$ , and $B = \begin{bmatrix} 24 \\ 40 \\ -10 \end{bmatrix}$ .

This equation can be restated as

$A^{-1}(AX) =A^{-1} B$

$(A^{-1}A)X =A^{-1} B$

$IX =A^{-1} B$

$X =A^{-1} B$

We are already given $A^{-1}$ , so:

$X =A^{-1} B$

$X = \begin{bmatrix} 8 &9 & -11 \\ 5 & 6 & -7 \\ 1 & 1 & -1 \end{bmatrix} \begin{bmatrix} 24 \\ 40 \\ -10 \end{bmatrix}$

Multiply two matrices by multiplying the rows in the first by the column in the second; this is done by adding the products of entries in corresponding positions, as follows:

$X = \begin{bmatrix} 8 (24)+9(40) +( -11)(-10) \\ 5(24) + 6(40) +( -7)(-10) \\ 1 (24)+ 1(40 )+( -1)(-10) \end{bmatrix}$

$X = \begin{bmatrix} 662 \\ 430 \\ 74 \end{bmatrix}$

We are only interested in the value of , which is 430.

Report an Error

Example Question #21 : Systems Of Linear Equations: Matrices

It is suggested (but not necessary) that you use a calculator with matrix capability to work this problem.

A village is famous for being the most prolific producer in the world of ambrosia, butterbeer, and silphium. Every year, they try to meet the world's demand for 20,000 kg of ambrosia, 30,000 kg of butterbeer, and 15,000 kg of silphium. However, the production of these items requires the consumption of these items as well:

The production of 1 kg of ambrosia requires the use of 0.05 kg of butterbeer and 0.08 kg of silphium;

The production of 1 kg of butterbeer requires the use of 0.04 kg of ambrosia and 0.09 kg of silphium; and,

The production of 1 kg of silphium requires the use of 0.06 kg of ambrosia and 0.07 kg of butterbeer.

Use a Leontief model to determine how much silphium (nearest hundred kilograms) must be produced to meet the demand.

Possible Answers:

$18,600 \textup{ kg }$

$18,700 \textup{ kg }$

$18,500 \textup{ kg }$

$18,400 \textup{ kg }$

$18,800 \textup{ kg }$

Correct answer:

$18,700 \textup{ kg }$

Explanation:

The Leontief model for an input-output system requires the following steps.

Let be the technology matrix for the system, the entries of which are the amounts of each product consumed in the manufacture of each product. Letting the rows/columns represent, in order, ambrosia, butterbeer, and silphium,

$A = \begin{bmatrix} 0 & 0.05 & 0.08 \\ 0.04 & 0 & 0.09 \\ 0.06 & 0.07 & 0\end{bmatrix}$

Let be the external demand vector, which gives the amount of each product demanded by outside consumers:

$D= \begin{bmatrix} 20,000 \\ 30,000 \\ 15,000 \end{bmatrix}$

The output vector , which gives the amount of each product that must be produced to meet the demand, can be obtained through the matrix equation

$X = (I- A )^{-1}D$

$= \left ( \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} - \begin{bmatrix} 0 & 0.05 & 0.08 \\ 0.04 & 0 & 0.09 \\ 0.06 & 0.07 & 0\end{bmatrix} \right )^{-1} \begin{bmatrix} 20,000 \\ 30,000 \\ 15,000 \end{bmatrix}$

$= \begin{bmatrix} 1 &-0.05 & -0.08 \\ -0.04 & 1 & -0.09 \\ -0.06 & -0.07 & 1 \end{bmatrix} ^{-1} \begin{bmatrix} 20,000 \\ 30,000 \\ 15,000 \end{bmatrix}$

$\approx \begin{bmatrix} 1.007394521 &0.056366243 & 0.085664523 \\0.046025673 & 1.008915193 & 0.094484421 \\ 0.063665468 & 0.074006038 &1.011753781 \end{bmatrix} \begin{bmatrix} 20,000 \\ 30,000 \\ 15,000 \end{bmatrix}$

$\approx \begin{bmatrix} 23,123.85 \\ 32,605.24\\ 18,669.80 \end{bmatrix}$

Silphium is represented by the bottom entry; the amount the village must produce rounds to 18,700 kg.

Report an Error

Example Question #31 : Finite Mathematics

It is suggested (but not necessary) that you use a calculator with matrix capability to work this problem.

The production of 1 kg of ambrosia requires the use of 0.05 kg of butterbeer and 0.08 kg of silphium;

The production of 1 kg of butterbeer requires the use of 0.04 kg of ambrosia and 0.09 kg of silphium; and,

The production of 1 kg of silphium requires the use of 0.06 kg of ambrosia and 0.07 kg of butterbeer.

Use a Leontief model to determine how much ambrosia (nearest hundred kilograms) must be produced to meet the demand.

Possible Answers:

$23,200 \textup{ kg}$

$23,500 \textup{ kg}$

$23,400 \textup{ kg}$

$23,300 \textup{ kg}$

$23,100 \textup{ kg}$

Correct answer:

$23,100 \textup{ kg}$

Explanation:

The Leontief model for an input-output system requires the following steps.

$A = \begin{bmatrix} 0 & 0.05 & 0.08 \\ 0.04 & 0 & 0.09 \\ 0.06 & 0.07 & 0\end{bmatrix}$

Let be the external demand vector, which gives the amount of each product demanded by outside consumers:

$D= \begin{bmatrix} 20,000 \\ 30,000 \\ 15,000 \end{bmatrix}$

The output vector , which gives the amount of each product that must be produced to meet the demand, can be obtained through the matrix equation

$X = (I- A )^{-1}D$

$= \begin{bmatrix} 1 &-0.05 & -0.08 \\ -0.04 & 1 & -0.09 \\ -0.06 & -0.07 & 1 \end{bmatrix} ^{-1} \begin{bmatrix} 20,000 \\ 30,000 \\ 15,000 \end{bmatrix}$

$\approx \begin{bmatrix} 23,123.85 \\ 32,605.24\\ 18,669.80 \end{bmatrix}$

Ambrosia is represented by the top entry; the amount the village must produce rounds to 23,100 kg.

Report an Error

Example Question #31 : Finite Mathematics

$A= \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}$

True or false: $A^{2} = \begin{bmatrix} 1 & 4 \\ 9 & 16 \end{bmatrix}$

Possible Answers:

False

True

Correct answer:

False

Explanation:

$A^{2} = AA=\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}$

Two matrices are multiplied by multiplying the rows of the first by the columns of the second - that is, adding the products of the entries in corresponding positions:

$A^{2} = \begin{bmatrix} 1(1)+2(3) & 1(2)+2(4) \\3(1)+4(3) & 3(2)+4(4) \end{bmatrix}$

$= \begin{bmatrix} 7 & 10 \\ 15 & 22 \end{bmatrix}$

$\ne \begin{bmatrix} 1 & 4 \\ 9 & 16 \end{bmatrix}$

The statement is false.

Report an Error

Example Question #32 : Finite Mathematics

$A= \begin{bmatrix}- \frac{4}{7} & \frac{2}{9} \\ \\ -\frac{5}{6}& \frac{3}{11} \end{bmatrix}$ and $B= \begin{bmatrix} \frac{5}{7} & \frac{2}{9} \\ \\ -\frac{5}{6}& -\frac{8}{11} \end{bmatrix}$ .

True or false: A- B = I , where is the two-by-two identity matrix.

Possible Answers:

True

False

Correct answer:

False

Explanation:

First, it must be established that A- B is defined. This is the case if and only and have the same number of rows, which is true, and they have the same number of columns, which is also true. A -B is therefore defined.

Subtraction of two matrices is performed by subtracting corresponding elements, so

$A-B= \begin{bmatrix}- \frac{4}{7} & \frac{2}{9} \\ \\ -\frac{5}{6}& \frac{3}{11} \end{bmatrix}- \begin{bmatrix} \frac{5}{7} & \frac{2}{9} \\ \\ -\frac{5}{6}& -\frac{8}{11} \end{bmatrix}$

$= \begin{bmatrix}- \frac{4}{7}-\frac{5}{7} & \frac{2}{9} - \frac{2}{9} \\ \\ -\frac{5}{6} - \left ( -\frac{5}{6} \right )& \frac{3}{11} -\left ( -\frac{8}{11} \right )\end{bmatrix}$

$= \begin{bmatrix} {\color{Red} -1} & 0 \\ 0 & 1 \end{bmatrix}$

However, $I = \begin{bmatrix} {\color{Red} 1 }& 0 \\ 0 & 1 \end{bmatrix}$ .

Therefore, $A-B \ne I$ .

Report an Error

Example Question #31 : Systems Of Linear Equations: Matrices

2x+ 5y = 17

4x-y = 13

Use Cramer's rule to evaluate .

Possible Answers:

$x= -\frac{59}{22}$

$x= \frac{21}{11}$

$x= \frac{41}{11}$

$x= -\frac{69}{22}$

None of the other choices gives the correct response.

Correct answer:

$x= \frac{41}{11}$

Explanation:

By Cramer's rule, the value of is equal to $x= \frac{D_{x}}{D}$ , where is the determinant of the matrix of coefficients

$D =\begin{vmatrix} 2 & 5 \\ 4 & -1 \end{vmatrix}$ ,

and $D_{x}$ is the same matrix with the x-coefficients replaced by the constants:

$D_{x}= \begin{vmatrix} 17 & 5 \\ 13 & -1 \end{vmatrix}$

The determinant of a two-by-two matrix is equal to the product of the entries in the main diagonal minus the product of the other two entries. Therefore,

$D_{x}= \begin{vmatrix} 17 & 5 \\ 13 & -1 \end{vmatrix} = 17(-1)-5(13)= -17 -65 = -82$

$D= \begin{vmatrix} 2 & 5 \\ 4 & -1 \end{vmatrix} = 2(-1) - 5(4) = -2 - 20 = -22$

and

$x= \frac{D_{x}}{D} = \frac{-82}{-22} = \frac{41}{11}$ .

Report an Error

Example Question #32 : Finite Mathematics

The initial simplex tableau for a minimization linear programming problem is given below:

$\begin{bmatrix} 2 & 3 & 2 &1 & 0 & 0 & 1,200 \\ 1 & 2 & 4 & 0 & 1 & 0 & 600\\ 0 & 4 & 3 & 0 & 0 & 1 & 900 \\ -1 & -1 & -2 & 0&0&0 & 0 \end{bmatrix}$

After the first pivot of the simplex method is performed, what will be the entry at bottom right?

Possible Answers:

300

600

400

1,200

Correct answer:

300

Explanation:

First, the pivot element must be identified. Select the pivot column by spotting the "most negative" element in the bottom, or objective, row. This is the in Column 3, making that the pivot column.

$\begin{bmatrix} 2 & 3 & 2 &1 & 0 & 0 & 1,200 \\ 1 & 2 & 4 & 0 & 1 & 0 & 600\\ 0 & 4 & 3 & 0 & 0 & 1 & 900 \\ -1 & -1 & {\color{Red} \textbf{-2}} & 0&0&0 & 0 \end{bmatrix}$

Select the pivot row by dividing the rightmost element in each other row by the pivot-column element in that row. The "least positive" quotient determines the pivot row:

$\begin{bmatrix} 2 & 3 & {\color{Blue} \textbf{2}} &1 & 0 & 0 & {\color{Blue} \textbf{1,200}} \\ 1 & 2 & {\color{Blue} \textbf{4}} & 0 & 1 & 0 & {\color{Blue} \textbf{600}}\\ 0 & 4 & {\color{Blue} \textbf{3}} & 0 & 0 & 1 & {\color{Blue} \textbf{900}} \\ -1 & -1 & {\color{Red} \textbf{-2}} & 0&0&0 & 0 \end{bmatrix}\begin{matrix} 1,200 \div 2 = 600 \\ 600 \div 4 = {\color{Red} \textbf{150}} \\ 900 \div 3 = 300\\\; \end{matrix}$

The "least positive" of the three quotients is 150, in Row 2. The pivot element is the 4 in Row 2, Column 3.

Perform the pivot by first multiplying each entry in Row 2 by $\frac{1}{4}$ in order to make the pivot element a 1:

$\frac{1}{4}R2\rightarrow R2$

$\begin{bmatrix} 2 & 3 & 2 &1 & 0 & 0 & 1,200 \\ \frac{1}{4} & \frac{1}{2} & 1 & 0 & \frac{1}{4} & 0 & 150\\ 0 & 4 & 3 & 0 & 0 & 1 & 900 \\ -1 & -1 & -2 & 0&0&0 & 0 \end{bmatrix}$

Make the other elements in that column zeroes by adding multiples of the pivot row to the other rows, as follows:

$-2R2 + R 1 \rightarrow R1$

$-3R2 + R3 \rightarrow R3$

$2R2 + R4 \rightarrow R4$

$\begin{bmatrix} \frac{3}{2} & 2 & 0 &1 & -\frac{1}{2} & 0 & 900 \\ \frac{1}{4} & \frac{1}{2} & 1 & 0 & \frac{1}{4} & 0 & 150\\ -\frac{3}{4} & \frac{5}{2} & 0 & 0 & -\frac{3}{4} & 1 & 450 \\ -\frac{1}{2} & 0& 0 & 0&\frac{1}{2}&0 & {\color{Red} \textbf{300}} \end{bmatrix}$

The entry at bottom right is 300.

Report an Error

Example Question #1 : Linear Inequalities And Linear Programming

The graph depicts which inequality?

Possible Answers:

x>-4

$x\leq-4$

x=-4

x<-4

$x\geq-4$

Correct answer:

x>-4

Explanation:

To identify the inequality the graph represents first identify range.

Since the red line goes from negative four to infinity, we can right this in mathematical terms as follows,

x>-4

Now, the inequality will remain a greater than sign because there is an open circle at four.

This means that does not equal four, it only equals values greater than four.

Thus, the correct inequality is

x>-4

Report an Error

Example Question #1 : Linear Inequalities And Linear Programming

The initial simplex tableau for a maximization linear programming problem is

$\begin{bmatrix} 1 & 3 & 1 & 0 & 540 \\ 2 & 1 & 0 & 1 & 200 \\ -4 & -7 & 0 & 0 & 0 \end{bmatrix}$

Locate the first pivot element.

Possible Answers:

Row 1, Column 1

Row 1, Column 2

Row 2, Column 2

Row 2, Column 1

Correct answer:

Row 1, Column 2

Explanation:

To select the pivot element while working a maximization problem, first, identify the pivot column by selecting the "most negative" element in the bottom, or objective, row. In the initial tableau, it is the in Column 2:

$\begin{bmatrix} 1 & 3 & 1 & 0 & 540 \\ 2 & 1 & 0 & 1 & 200 \\ -4 & \textbf{{\color{Red} -7}} & 0 & 0 & 0 \end{bmatrix}$

In the other rows, divide the rightmost element by the element in the pivot column. The pivot row is identified by selecting the "least positive" quotient.

$\begin{bmatrix} 1 & 3 & 1 & 0 & 540 \\ 2 & 1 & 0 & 1 & 200 \\ -4 & \textbf{{\color{Red} -7}} & 0 & 0 & 0 \end{bmatrix}\begin{matrix} 540 \div 3 = \textbf{180 }\\ 200 \div 1 = 200 \\ \; \end{matrix}$

The least positive quotient appears in Row 1. This puts the pivot element in Row 1, Column 2.

Report an Error

← Previous 1 2 3 4 5 6 7 8 9 10 11 Next →

View Tutors

Bianca
Certified Tutor

Central New Mexico Community College, Associate in Science, Diagnostic Medical Sonography.

View Tutors

Morgan
Certified Tutor

York University, Bachelor in Arts, Communication, General. University of Essex, Master of Fine Arts, Directing and Theatrical...

View Tutors

Odysseas
Certified Tutor

University of New Hampshire at Manchester, Master of Science, Civil Engineering. National Technical University of Athens, Doc...

All Finite Mathematics Resources

1 Diagnostic Test 22 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SSAT Tutors in Philadelphia, Math Tutors in Boston, Computer Science Tutors in San Diego, Calculus Tutors in Washington DC, Computer Science Tutors in Chicago, Chemistry Tutors in Atlanta, LSAT Tutors in Houston, Algebra Tutors in San Diego, MCAT Tutors in San Francisco-Bay Area, Algebra Tutors in Houston

Popular Courses & Classes

GRE Courses & Classes in Miami, ACT Courses & Classes in Phoenix, SAT Courses & Classes in Philadelphia, SSAT Courses & Classes in Phoenix, MCAT Courses & Classes in Washington DC, GMAT Courses & Classes in Phoenix, GRE Courses & Classes in Washington DC, Spanish Courses & Classes in San Francisco-Bay Area, SSAT Courses & Classes in Philadelphia, GMAT Courses & Classes in Boston

Popular Test Prep

GRE Test Prep in Miami, GMAT Test Prep in Atlanta, GRE Test Prep in Los Angeles, SSAT Test Prep in San Francisco-Bay Area, SSAT Test Prep in Washington DC, MCAT Test Prep in Los Angeles, SAT Test Prep in Washington DC, GMAT Test Prep in Miami, ACT Test Prep in New York City, GMAT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Finite Mathematics : Finite Mathematics

Study concepts, example questions & explanations for Finite Mathematics

All Finite Mathematics Resources

Example Questions

Example Question #1 : Solve A System Of Equations In Three Variables Using Augmented Matrices

Example Question #31 : Finite Mathematics

Example Question #21 : Systems Of Linear Equations: Matrices

Example Question #31 : Finite Mathematics

Example Question #31 : Finite Mathematics

Example Question #32 : Finite Mathematics

Example Question #31 : Systems Of Linear Equations: Matrices

Example Question #32 : Finite Mathematics

Example Question #1 : Linear Inequalities And Linear Programming

Example Question #1 : Linear Inequalities And Linear Programming

All Finite Mathematics Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: