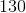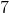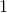Call Now to Set Up Tutoring:

(888) 888-0446

Complex Analysis : Complex Numbers

Study concepts, example questions & explanations for Complex Analysis

Create An Account

All Complex Analysis Resources

1 Diagnostic Test 13 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #11 : Complex Numbers

Evaluate:

$\left| ( 8 + 5 i ) ( -10 + 3 i ) \right|$

Possible Answers:

$\sqrt{9701}$

$- \sqrt{9701}$

9701

$\frac{\sqrt{9701}}{2}$

Correct answer:

$\sqrt{9701}$

Explanation:

The general formula to figure out the modulus is

$\left|a+bi\right|=\sqrt{a^2+b^2}$

We apply this to get

$\left| ( 8 + 5 i ) ( -10 + 3 i ) \right| = \sqrt{ 64 + 25 }\cdot \sqrt{ 100 + 9 }$

$= \sqrt{89} \cdot \sqrt{109}$

$= \sqrt{9701}$

Report an Error

Example Question #12 : Complex Numbers

Evaluate: $\left| 9 - 7 i \right|$

Possible Answers:

130

$\sqrt{130}$

$-\sqrt{130}$

Correct answer:

$\sqrt{130}$

Explanation:

The general formula to figure out the modulus is

$\left|a+bi\right|=\sqrt{a^2+b^2}$ .

We apply this notion to get.

$\left| 9 - 7 i \right| = \sqrt{ 81 + 49 }$

$= \sqrt{130}$

Report an Error

Example Question #11 : Complex Numbers

Evaluate $(\sqrt{3} - i)^6$

Possible Answers:

-64

-64i

None of the other answers

64i

Correct answer:

-64

Explanation:

Converting from rectangular to polar coordinates gives us

$r = \sqrt{x^2+y^2} = \sqrt{3+1} = 2$

$\theta = tan^{-1}(y/x) = tan^{-1}\left(-\frac{1}{\sqrt{3}}\right) = -\frac{\pi}{6}$

$(\sqrt{3}-i)^6 = (2e^{-\frac{\pi}{6}i})^6 = 64e^{-\pi i} = -64$

Report an Error

Example Question #14 : Complex Numbers

Compute $(-16)^\frac{1}{4}$

Possible Answers:

$\pm\sqrt{2}(1-i)$

$\pm(\sqrt{3} - i) \text{ and } \pm(1+\sqrt{3}i)$

$\pm 2 \text{ and } \pm 2i$

$\pm\sqrt{2}(1+i)$

$\pm\sqrt{2}(1+i) \text{ and } \pm\sqrt{2}(1-i)$

Correct answer:

$\pm\sqrt{2}(1+i) \text{ and } \pm\sqrt{2}(1-i)$

Explanation:

Converting from Rectangular to Polar Coordinates

$(-16)^\frac{1}{4} = (16e^{i\pi + 2\pi k})^\frac{1}{4} = 2e^{i\frac{\pi}{4} + \frac{\pi}{2}k}$

Evaluating for k = 0,1,2,3

we get that

$\pm\sqrt{2}(1+i) \text{ and } \pm\sqrt{2}(1-i)$

Report an Error

Example Question #15 : Complex Numbers

The 5th roots of unity are the five unique solutions to which equation?

Possible Answers:

z^5-1=0

None of these

(z-1)^5=0

z^5+z^4+z^3+z^2+z+1=0

z^5+1=0

Correct answer:

z^5-1=0

Explanation:

A 5th root of unity is a complex number such that z^5=1 . Manipulating this equation yields z^5-1=0 .

Report an Error

Example Question #16 : Complex Numbers

What is the magnitude of the following complex number?

5+2i

Possible Answers:

$\sqrt{14}$

$\sqrt{29}$

None of these

Correct answer:

$\sqrt{29}$

Explanation:

The magnitude of a complex number a+bi is defined as

$\vert a+bi\vert=\sqrt{a^2+b^2}.$

So the modulus of 5+2i is

$\vert5+2i\vert=\sqrt{5^2+2^2}=\sqrt{25+4}=\sqrt{29}$ .

Report an Error

Example Question #14 : Complex Numbers

What is the magnitude of the following complex number?

3-i

Possible Answers:

$\sqrt{10}$

None of these

$\sqrt{8}$

Correct answer:

$\sqrt{10}$

Explanation:

The magnitude of a complex number a+bi is defined as

$\vert a+bi\vert=\sqrt{a^2+b^2}.$

So the modulus of 3-i is

$\vert3-i\vert=\sqrt{3^2+(-1)^2}=\sqrt{9+1}=\sqrt{10}$ .

Report an Error

Example Question #17 : Complex Numbers

What is the magnitude of the following complex number?

Possible Answers:

$2\sqrt2$

None of these

Correct answer:

Explanation:

The magnitude of a complex number a+bi is defined as

$\vert a+bi\vert=\sqrt{a^2+b^2}.$

Because the complex number has no imaginary part, we can write it in the form 8+0i . Then the modulus of 8+0i is

$\vert8+0i\vert=\sqrt{8^2+0^2}=\sqrt{64+0}=\sqrt{64}=8$ .

Report an Error

Example Question #18 : Complex Numbers

What is the argument of the following complex number?

1+i

Possible Answers:

$\frac{-3\pi}{4}$

$\frac{\pi}{4}$

None of these

$\frac{\pi}{2}$

Correct answer:

$\frac{\pi}{4}$

Explanation:

Note that the complex number 1+i lies in the first quadrant of the complex plane.

For a complex number z=a+bi , the argument of is defined as the real number $\theta$ such that

$\tan(\theta)=\frac{b}{a}$ ,

where $-\pi<\theta\leq\pi$ is in radians.

Then the argument of 1+i is

$\tan(\theta)=\frac{1}{1}=1$

$\theta=\frac{-3\pi}{4},\frac{\pi}{4}$ .

The angle $\frac{-3\pi}{4}$ lies in the third quadrant of the complex plane, but the angle $\frac{\pi}{4}$ lies in the first quadrant, as does 1+i . So $\theta=\frac{\pi}{4}$ .

Report an Error

Example Question #19 : Complex Numbers

What is the argument of the following complex number in radians, rounded to the nearest hundredth?

2-3i

Possible Answers:

3.61

None of these

-0.98

-0.59

2.16

Correct answer:

-0.98

Explanation:

Note that the complex number 2-3i lies in the fourth quadrant of the complex plane.

For a complex number z=a+bi , the argument of is defined as the real number $\theta$ such that

$\tan(\theta)=\frac{b}{a}$ ,

where $-\pi<\theta\leq\pi$ is in radians.

Then the argument of 2-3i is

$\tan(\theta)=\frac{-3}{2}$

$\theta=-0.98,2.16$ .

The angle 2.16 lies in the second quadrant of the complex plane, but the angle -0.98 lies in the fourth quadrant, as does 2-3i . So $\theta=-0.98$ .

Report an Error

View Tutors

Molly
Certified Tutor

Grand Valley State University, Bachelor of Fine Arts, Psychology. Western Michigan University, Master of Fine Arts, Psychology.

View Tutors

Marie
Certified Tutor

Silliman University, Master of Science, Mathematics.

View Tutors

Elizabeth
Certified Tutor

University of Oklahoma Norman Campus, Bachelor of Education, Education. University of Oklahoma Norman Campus, Master of Scien...

All Complex Analysis Resources

1 Diagnostic Test 13 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SAT Tutors in Philadelphia, Biology Tutors in Miami, Physics Tutors in Denver, French Tutors in Atlanta, Math Tutors in Phoenix, MCAT Tutors in Boston, GRE Tutors in Boston, ISEE Tutors in Los Angeles, Statistics Tutors in Denver, Reading Tutors in Philadelphia

Popular Courses & Classes

ACT Courses & Classes in Chicago, MCAT Courses & Classes in Phoenix, ACT Courses & Classes in Los Angeles, LSAT Courses & Classes in Washington DC, SSAT Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in Philadelphia, GMAT Courses & Classes in Boston, MCAT Courses & Classes in Denver, SAT Courses & Classes in New York City, GRE Courses & Classes in San Francisco-Bay Area

Popular Test Prep

LSAT Test Prep in Houston, ACT Test Prep in Chicago, SSAT Test Prep in Dallas Fort Worth, LSAT Test Prep in Denver, SSAT Test Prep in Denver, ACT Test Prep in Los Angeles, GRE Test Prep in Miami, MCAT Test Prep in Phoenix, MCAT Test Prep in Los Angeles, MCAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Complex Analysis : Complex Numbers

Study concepts, example questions & explanations for Complex Analysis

All Complex Analysis Resources

Example Questions

Example Question #11 : Complex Numbers

Example Question #12 : Complex Numbers

Example Question #11 : Complex Numbers

Example Question #14 : Complex Numbers

Example Question #15 : Complex Numbers

Example Question #16 : Complex Numbers

Example Question #14 : Complex Numbers

Example Question #17 : Complex Numbers

Example Question #18 : Complex Numbers

Example Question #19 : Complex Numbers

All Complex Analysis Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: