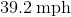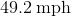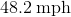All Common Core: High School - Number and Quantity Resources
Example Questions
Example Question #3 : Vector Components: Ccss.Math.Content.Hsn Vm.A.2
What are the components of a vector that has a terminal point of 

In order to determine what the components of this vector has, we need to remember how to find components of a vector. It's simply the difference between the terminal point and initial point. The first step is to write an equation for what our "new" x and y are.
Now lets identify what these values are.
To write this in component form, we need to put our 


So the final answer is
Below is a visual representation of what we just did.

Example Question #4 : Vector Components: Ccss.Math.Content.Hsn Vm.A.2
What are the components of a vector that has a terminal point of 

In order to determine what the components of this vector has, we need to remember how to find components of a vector. It's simply the difference between the terminal point and initial point. The first step is to write an equation for what our "new" x and y are.
Now lets identify what these values are.
To write this in component form, we need to put our 


So the final answer is
Below is a visual representation of what we just did.

Example Question #113 : High School: Number And Quantity
What are the components of a vector that has a terminal point of 

In order to determine what the components of this vector has, we need to remember how to find components of a vector. It's simply the difference between the terminal point and initial point. The first step is to write an equation for what our "new" x and y are.
Now lets identify what these values are.
To write this in component form, we need to put our 


So the final answer is
Below is a visual representation of what we just did.

Example Question #114 : High School: Number And Quantity
What are the components of a vector that has a terminal point of 

In order to determine what the components of this vector has, we need to remember how to find components of a vector. It's simply the difference between the terminal point and initial point. The first step is to write an equation for what our "new" x and y are.
Now lets identify what these values are.
To write this in component form, we need to put our 


So the final answer is
Below is a visual representation of what we just did.

Example Question #121 : High School: Number And Quantity
Bob is cruising south down a river at 

Not possible to find
In order to figure this out, we need to create a picture.


Since bob is traveling south, and the current is traveling west, they are perpendicular to each other. This means that they are 
Recall that the Pythagorean Theorem is 





For our calculations, let 

Example Question #2 : Vector Representation Of Quantities (Velocity, Etc.): Ccss.Math.Content.Hsn Vm.A.3
Amanda is cruising north down a river at 

In order to figure this out, we need to create a picture.

Since Amanda is traveling north, and the current is traveling east, they are perpendicular to each other. This means that they are 
Recall that the Pythagorean Theorem is 





For our calculations, let 

Example Question #3 : Vector Representation Of Quantities (Velocity, Etc.): Ccss.Math.Content.Hsn Vm.A.3
Jack slides down a hill at 

Since the rock is going in the opposite direction of Jack, we simply subtract the speed of the rock from how fast Jack is going down the hill.
Example Question #4 : Vector Representation Of Quantities (Velocity, Etc.): Ccss.Math.Content.Hsn Vm.A.3
If an airplane is flying south at 

In order to figure this out, we need to create a picture.

Since the airplane is traveling south, and the wind is coming from the west, they are perpendicular to each other. This means that they are 
Recall that the Pythagorean Theorem is 





For our calculations, let 

Example Question #122 : High School: Number And Quantity
Jill slides down a hill at 


Since the coin is going in the same direction as Jill, we simply add the speed of the coin and how fast Jill is going down the hill.
Example Question #6 : Vector Representation Of Quantities (Velocity, Etc.): Ccss.Math.Content.Hsn Vm.A.3
Bob slides down a hill at 

Since Bob's wallet is going in the opposite direction, we simply subtract the speed of the wallet from how fast Bob is going down the hill.
All Common Core: High School - Number and Quantity Resources