Common Core: High School - Functions : Interpreting Functions
Study concepts, example questions & explanations for Common Core: High School - Functions
All Common Core: High School - Functions Resources
Example Questions
Example Question #9 : Graph Linear And Quadratic Functions: Ccss.Math.Content.Hsf If.C.7a
What is the 
This question tests one's ability to recognize algebraic characteristics of a graph. This particular question examines a quadratic function.
For the purpose of Common Core Standards, "graph linear and quadratic functions and show intercepts, maxima, and minima" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify the general algebraic function for the given graph.
Since the graph is that of a parabola opening up, the general algebraic form of the function is,
where
Recall that if 
Step 2: Identify where the graph crosses the 
For the function above, the vertex is also the minimum of the function and lies at the 
Therefore the vertex lies at 
Step 3: Answer the question.
The
Example Question #10 : Graph Linear And Quadratic Functions: Ccss.Math.Content.Hsf If.C.7a
What is the
This question tests one's ability to recognize algebraic characteristics of a graph. This particular question examines a quadratic function.
For the purpose of Common Core Standards, "graph linear and quadratic functions and show intercepts, maxima, and minima" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify the general algebraic function for the given graph.
Since the graph is that of a parabola opening up, the general algebraic form of the function is,
where
Recall that if 
Step 2: Identify where the graph crosses the
For the function above, the vertex is also the minimum of the function and lies at the 
Therefore the vertex lies at 
Step 3: Answer the question.
The
Example Question #11 : Graph Linear And Quadratic Functions: Ccss.Math.Content.Hsf If.C.7a
What is the
This question tests one's ability to recognize algebraic characteristics of a graph. This particular question examines a quadratic function.
For the purpose of Common Core Standards, "graph linear and quadratic functions and show intercepts, maxima, and minima" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify the general algebraic function for the given graph.
Since the graph is that of a parabola opening up, the general algebraic form of the function is,
where
Recall that if 
Step 2: Identify where the graph crosses the
For the function above, the parabola is shifted to the right therefore the 
Therefore the 
Step 3: Answer the question.
The
Example Question #82 : High School: Functions
What is the
This question tests one's ability to recognize algebraic characteristics of a graph. This particular question examines a quadratic function.
For the purpose of Common Core Standards, "graph linear and quadratic functions and show intercepts, maxima, and minima" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify the general algebraic function for the given graph.
Since the graph is that of a parabola opening up, the general algebraic form of the function is,
where
Recall that if 
Step 2: Identify where the graph crosses the
For the function above, the parabola is shifted to the right therefore the 
Therefore the 
Step 3: Answer the question.
The
Example Question #1 : Graph Square Root, Cube Root, And Piecewise Functions: Ccss.Math.Content.Hsf If.C.7b
Graph the following function
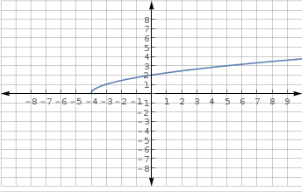
This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of 
The values in the table are found by substituting in the x values into the function as follows.
Step 2: Plot the points on a coordinate grid
Step 3: Connect the points with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values less than negative four will be in the domain.
Example Question #2 : Graph Square Root, Cube Root, And Piecewise Functions: Ccss.Math.Content.Hsf If.C.7b
Graph the following function.
This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of
The values in the table are found by substituting in the x values into the function as follows.
Step 2: Plot the points on a coordinate grid
Step 3: Connect the points with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values more than two will be in the domain.
Example Question #3 : Graph Square Root, Cube Root, And Piecewise Functions: Ccss.Math.Content.Hsf If.C.7b
Graph the following function.
This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of
The values in the table are found by substituting in the x values into the function as follows.
Step 2: Plot the points on a coordinate grid
Step 3: Connect the points with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values greater than one will be in the domain.
Example Question #4 : Graph Square Root, Cube Root, And Piecewise Functions: Ccss.Math.Content.Hsf If.C.7b
Graph the following function.
This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of
The values in the table are found by substituting in the x values into the function as follows.
Step 2: Plot the points on a coordinate grid and connect them with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values less than zero will be in the domain.
Example Question #5 : Graph Square Root, Cube Root, And Piecewise Functions: Ccss.Math.Content.Hsf If.C.7b
Graph the following function.
This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of
The values in the table are found by substituting in the x values into the function as follows.
Step 2: Plot the points on a coordinate grid and connect them with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values less than negative two will be in the domain.
Example Question #6 : Graph Square Root, Cube Root, And Piecewise Functions: Ccss.Math.Content.Hsf If.C.7b
Graph the following function.
This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of
The values in the table are found by substituting in the x values into the function as follows.
Step 2: Plot the points on a coordinate grid and connect them with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values less than two will be in the domain.
All Common Core: High School - Functions Resources
