Common Core: High School - Functions : High School: Functions
Study concepts, example questions & explanations for Common Core: High School - Functions
All Common Core: High School - Functions Resources
Example Questions
Example Question #7 : Graph Square Root, Cube Root, And Piecewise Functions: Ccss.Math.Content.Hsf If.C.7b
Graph the following function.
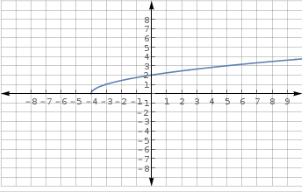
This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of 
The values in the table are found by substituting in the x values into the function as follows.
Step 2: Plot the points on a coordinate grid and connect them with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values less than three will be in the domain.
Example Question #8 : Graph Square Root, Cube Root, And Piecewise Functions: Ccss.Math.Content.Hsf If.C.7b
Graph the following function.
This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of
The values in the table are found by substituting in the x values into the function as follows.
Step 2: Plot the points on a coordinate grid and connect them with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values less than zero will be in the domain.
Example Question #9 : Graph Square Root, Cube Root, And Piecewise Functions: Ccss.Math.Content.Hsf If.C.7b
Graph the following function.
This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of
The values in the table are found by substituting in the x values into the function as follows.
Step 2: Plot the points on a coordinate grid and connect them with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values less than zero will be in the domain.
Example Question #10 : Graph Square Root, Cube Root, And Piecewise Functions: Ccss.Math.Content.Hsf If.C.7b
Graph the following function.
This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of
The values in the table are found by substituting in the x values into the function as follows.
Step 2: Plot the points on a coordinate grid and connect them with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values less than one half will be in the domain.
Example Question #91 : High School: Functions
Graph the following function.
This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of
The values in the table are found by substituting in the x values into the function as follows.
Step 2: Plot the points on a coordinate grid and connect them with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values greater than zero will be in the domain.
Example Question #92 : High School: Functions
Graph the following function.
This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of
The values in the table are found by substituting in the x values into the function as follows.
Step 2: Plot the points on a coordinate grid and connect them with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values greater than zero will be in the domain.
Example Question #1 : Graph Polynomial Functions, Identify Zeros, Factor, And Identify End Behavior.: Css.Math.Content.Hsf If.C.7c
Graph the following function and identify the zeros.
This question tests one's ability to graph a polynomial function.
For the purpose of Common Core Standards, "graph polynomial functions, identifying zeros when suitable factorizations are available, and showing end behavior" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Use algebraic technique to factor the function.
Separating the function into two parts...
Factoring a negative one from the second set results in...
Factoring out 
The new factored form of the function is,
Now, recognize that the first binomial is a perfect square for which the following formula can be used
since
thus the simplified, factored form is,
Step 2: Identify the roots of the function.
To find the roots of a function set its factored form equal to zero and solve for the possible x values.
Step 3: Create a table of 
The values in the table are found by substituting in the x values into the function as follows.
Step 4: Plot the points on a coordinate grid and connect them with a smooth curve.
Example Question #1 : Graph Polynomial Functions, Identify Zeros, Factor, And Identify End Behavior.: Css.Math.Content.Hsf If.C.7c
Graph the function and identify its roots.
This question tests one's ability to graph a polynomial function.
For the purpose of Common Core Standards, "graph polynomial functions, identifying zeros when suitable factorizations are available, and showing end behavior" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Use algebraic technique to factor the function.
Recognize that the binomial is a perfect square for which the following formula can be used
since
thus the simplified, factored form is,
Step 2: Identify the roots of the function.
To find the roots of a function set its factored form equal to zero and solve for the possible x values.
Step 3: Create a table of
The values in the table are found by substituting in the x values into the function as follows.
Step 4: Plot the points on a coordinate grid and connect them with a smooth curve.
Example Question #2 : Graph Polynomial Functions, Identify Zeros, Factor, And Identify End Behavior.: Css.Math.Content.Hsf If.C.7c
Graph the function and identify the roots.
This question tests one's ability to graph a polynomial function.
For the purpose of Common Core Standards, "graph polynomial functions, identifying zeros when suitable factorizations are available, and showing end behavior" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Use algebraic technique to factor the function.
Recognize that the binomial is a perfect square for which the following formula can be used
since
thus the simplified, factored form is,
Step 2: Identify the roots of the function.
To find the roots of a function set its factored form equal to zero and solve for the possible x values.
Step 3: Create a table of
The values in the table are found by substituting in the x values into the function as follows.
Step 4: Plot the points on a coordinate grid and connect them with a smooth curve.
Example Question #6 : Graph A Polynomial Function
Graph the function and identify its roots.
This question tests one's ability to graph a polynomial function.
For the purpose of Common Core Standards, "graph polynomial functions, identifying zeros when suitable factorizations are available, and showing end behavior" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Use algebraic technique to factor the function.
Recognize that the binomial is a perfect square for which the following formula can be used
since
thus the simplified, factored form is,
Step 2: Identify the roots of the function.
To find the roots of a function set its factored form equal to zero and solve for the possible x values.
Step 3: Create a table of
The values in the table are found by substituting in the x values into the function as follows.
Step 4: Plot the points on a coordinate grid and connect them with a smooth curve.
All Common Core: High School - Functions Resources
