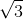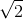All Common Core: 8th Grade Math Resources
Example Questions
Example Question #11 : Grade 8
Which of the following is an irrational number?
An irrational number is any number that cannot be expressed as a ratio of integers.
Therefore, 
Example Question #11 : Grade 8
Which of the following is an irrational number?
A rational number is any number that can be expressed as a fraction where both the numerator and denominator are integers. The denominator also cannot be equal to 0. In this set, the irrational number is 
Example Question #12 : Grade 8
Which of the following answer choices displays a rational number?
Our answer choices consist of two types of numbers: rational numbers and irrational numbers. In order to correctly answer this question, we need to know the difference between the two types of numbers.
Rational numbers are numbers that we use most often, and can be written as a simple fraction.
Irrational numbers cannot be written as fractions, and are numbers that have decimal places that never repeat or end.
In this case, 
Example Question #12 : Grade 8
Which of the following answer choices displays a rational number?
Our answer choices consist of two types of numbers: rational numbers and irrational numbers. In order to correctly answer this question, we need to know the difference between the two types of numbers.
Rational numbers are numbers that we use most often, and can be written as a simple fraction.
Irrational numbers cannot be written as fractions, and are numbers that have decimal places that never repeat or end.
In this case, 
Example Question #15 : Understand The Difference Between Rational And Irrational Numbers: Ccss.Math.Content.8.Ns.A.1
Which of the following answer choices displays a rational number?
Our answer choices consist of two types of numbers: rational numbers and irrational numbers. In order to correctly answer this question, we need to know the difference between the two types of numbers.
Rational numbers are numbers that we use most often, and can be written as a simple fraction.
Irrational numbers cannot be written as fractions, and are numbers that have decimal places that never repeat or end.
In this case, 
Example Question #12 : Grade 8
Which of the following answer choices displays a rational number?
Our answer choices consist of two types of numbers: rational numbers and irrational numbers. In order to correctly answer this question, we need to know the difference between the two types of numbers.
Rational numbers are numbers that we use most often, and can be written as a simple fraction.
Irrational numbers cannot be written as fractions, and are numbers that have decimal places that never repeat or end.
In this case, 

Example Question #12 : Understand The Difference Between Rational And Irrational Numbers: Ccss.Math.Content.8.Ns.A.1
Which of the following answer choices displays a rational number?
Our answer choices consist of two types of numbers: rational numbers and irrational numbers. In order to correctly answer this question, we need to know the difference between the two types of numbers.
Rational numbers are numbers that we use most often, and can be written as a simple fraction.
Irrational numbers cannot be written as fractions, and are numbers that have decimal places that never repeat or end.
In this case, 

Example Question #15 : Grade 8
Which of the following answer choices displays a rational number?
Our answer choices consist of two types of numbers: rational numbers and irrational numbers. In order to correctly answer this question, we need to know the difference between the two types of numbers.
Rational numbers are numbers that we use most often, and can be written as a simple fraction.
Irrational numbers cannot be written as fractions, and are numbers that have decimal places that never repeat or end.
In this case, 
Example Question #11 : Understand The Difference Between Rational And Irrational Numbers: Ccss.Math.Content.8.Ns.A.1
Which of the following answer choices displays an irrational number?
Our answer choices consist of two types of numbers: rational numbers and irrational numbers. In order to correctly answer this question, we need to know the difference between the two types of numbers.
Rational numbers are numbers that we use most often, and can be written as a simple fraction.
Irrational numbers cannot be written as fractions, and are numbers that have decimal places that never repeat or end.
In this case, 
Example Question #19 : Understand The Difference Between Rational And Irrational Numbers: Ccss.Math.Content.8.Ns.A.1
Which of the following answer choices displays an irrational number?
Our answer choices consist of two types of numbers: rational numbers and irrational numbers. In order to correctly answer this question, we need to know the difference between the two types of numbers.
Rational numbers are numbers that we use most often, and can be written as a simple fraction.
Irrational numbers cannot be written as fractions, and are numbers that have decimal places that never repeat or end.
In this case, 
All Common Core: 8th Grade Math Resources