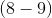All Common Core: 8th Grade Math Resources
Example Questions
Example Question #1 : Understand That The Solution Of A System Of Two Linear Equations Is The Intersection Of Their Lines: Ccss.Math.Content.8.Ee.C.8a
Identify the point of intersection by solving for the solution of the system of equations in the provided figure.

The graph displays a system of two linear equations. The point where these two lines intersect is the solution to the system of the equations because that coordinate point is the point that both lines have in common, or pass through.
In this case, the solution to the two linear equations that are displayed in the graph is the following point:
Example Question #192 : Grade 8
Identify the point of intersection by solving for the solution of the system of equations in the provided figure.

The graph displays a system of two linear equations. The point where these two lines intersect is the solution to the system of the equations because that coordinate point is the point that both lines have in common, or pass through.
In this case, the solution to the two linear equations that are displayed in the graph is the following point:
Example Question #2 : Understand That The Solution Of A System Of Two Linear Equations Is The Intersection Of Their Lines: Ccss.Math.Content.8.Ee.C.8a
Identify the point of intersection by solving for the solution of the system of equations in the provided figure.

The graph displays a system of two linear equations. The point where these two lines intersect is the solution to the system of the equations because that coordinate point is the point that both lines have in common, or pass through.
In this case, the solution to the two linear equations that are displayed in the graph is the following point:
Example Question #194 : Grade 8
Identify the point of intersection by solving for the solution of the system of equations in the provided figure.

The graph displays a system of two linear equations. The point where these two lines intersect is the solution to the system of the equations because that coordinate point is the point that both lines have in common, or pass through.
In this case, the solution to the two linear equations that are displayed in the graph is the following point:
Example Question #195 : Grade 8
Identify the point of intersection by solving for the solution of the system of equations in the provided figure.

The graph displays a system of two linear equations. The point where these two lines intersect is the solution to the system of the equations because that coordinate point is the point that both lines have in common, or pass through.
In this case, the solution to the two linear equations that are displayed in the graph is the following point:
Example Question #196 : Grade 8
Identify the point of intersection by solving for the solution of the system of equations in the provided figure.

The graph displays a system of two linear equations. The point where these two lines intersect is the solution to the system of the equations because that coordinate point is the point that both lines have in common, or pass through.
In this case, the solution to the two linear equations that are displayed in the graph is the following point:
Example Question #197 : Grade 8
Identify the point of intersection by solving for the solution of the system of equations in the provided figure.

The graph displays a system of two linear equations. The point where these two lines intersect is the solution to the system of the equations because that coordinate point is the point that both lines have in common, or pass through.
In this case, the solution to the two linear equations that are displayed in the graph is the following point:
Example Question #198 : Grade 8
Identify the point of intersection by solving for the solution of the system of equations in the provided figure.

The graph displays a system of two linear equations. The point where these two lines intersect is the solution to the system of the equations because that coordinate point is the point that both lines have in common, or pass through.
In this case, the solution to the two linear equations that are displayed in the graph is the following point:
Example Question #199 : Grade 8
Identify the point of intersection by solving for the solution of the system of equations graphed in the provided figure.

The graph displays a system of two linear equations. The point where these two lines intersect is the solution to the system of the equations because that coordinate point is the point that both lines have in common, or pass through.
In this case, the solution to the two linear equations that are displayed in the graph is the following point:
Example Question #1 : How To Find The Solution For A System Of Equations
Solve the system for 

The most simple method for solving systems of equations is to transform one of the equations so it allows for the canceling out of a variable. In this case, we can multiply 


Then, we can add 


We can plug that value into either of the original equations; for example, 
So, 
All Common Core: 8th Grade Math Resources