All Common Core: 8th Grade Math Resources
Example Questions
Example Question #1 : Solve Systems Of Two Linear Equations: Ccss.Math.Content.8.Ee.C.8b
Solve the set of equations:
Solve the first equation for 
Substitute into the second equation:
Multiply the entire equation by 2 to eliminate the fraction:
Using the value of 

Therefore, the solution is
Example Question #1 : Solve Systems Of Two Linear Equations: Ccss.Math.Content.8.Ee.C.8b
Solve the following system of equations:
Set the two equations equal to one another:
2x - 2 = 3x + 6
Solve for x:
x = -8
Plug this value of x into either equation to solve for y. We'll use the top equation, but either will work.
y = 2 * (-8) - 2
y = -18
Example Question #2 : Solve Systems Of Two Linear Equations: Ccss.Math.Content.8.Ee.C.8b
Solve this system of equations for 
None of the other choices are correct.
Multiply the bottom equation by 
Divide both sides by
Example Question #201 : Systems Of Equations
Solve the following system of equations:
infinitely many solutions
no solution
When we add the two equations, the 
Solving for 
We can then substitute our value for 

Example Question #211 : Grade 8
Solve the following system of equations.
We are given
We can solve this by using the substitution method. Notice that you can plug 
Add 
Add 9 to both sides
Divide both sides by 5
So 

So the solution is
Example Question #212 : Grade 8
Use algebra to solve the following system of linear equations:
There are a couple of ways to solve a system of linear equations: graphically and algebraically. In this lesson, we will review the two ways to solve a system of linear equations algebraically: substitution and elimination.
Substitution can be used by solving one of the equations for either 


Elimination is best used when one of the variables has the same coefficient in both equations, because you can then use addition or subtraction to cancel one of the variables out, and solve for the other variable.
For this problem, elimination makes the most sense because our 
Next, we can divide both sides by 
Remember, when we are solving a system of linear equations, we are looking for the point of intersection; thus, our answer should have both 

Now that we have the value of 

We want to subtract 
Our point of intersection, and the solution to the two system of linear equations is
Example Question #172 : Expressions & Equations
Use algebra to solve the following system of linear equations:
There are a couple of ways to solve a system of linear equations: graphically and algebraically. In this lesson, we will review the two ways to solve a system of linear equations algebraically: substitution and elimination.
Substitution can be used by solving one of the equations for either 


Elimination is best used when one of the variables has the same coefficient in both equations, because you can then use addition or subtraction to cancel one of the variables out, and solve for the other variable.
For this problem, elimination makes the most sense because our 
Next, we can divide both sides by 
Remember, when we are solving a system of linear equations, we are looking for the point of intersection; thus, our answer should have both 

Now that we have the value of 

We want to add 
Then we divide each side by
Our point of intersection, and the solution to the two system of linear equations is
Example Question #173 : Expressions & Equations
Use algebra to solve the following system of linear equations:
There are a couple of ways to solve a system of linear equations: graphically and algebraically. In this lesson, we will review the two ways to solve a system of linear equations algebraically: substitution and elimination.
Substitution can be used by solving one of the equations for either 


Elimination is best used when one of the variables has the same coefficient in both equations, because you can then use addition or subtraction to cancel one of the variables out, and solve for the other variable.
For this problem, elimination makes the most sense because our 
Next, we can divide both sides by 
Remember, when we are solving a system of linear equations, we are looking for the point of intersection; thus, our answer should have both 

Now that we have the value of 

We want to subtract 
Then divide both sides by 
Our point of intersection, and the solution to the two system of linear equations is
Example Question #215 : Grade 8
Use algebra to solve the following system of linear equations:
There are a couple of ways to solve a system of linear equations: graphically and algebraically. In this lesson, we will review the two ways to solve a system of linear equations algebraically: substitution and elimination.
Substitution can be used by solving one of the equations for either 


Elimination is best used when one of the variables has the same coefficient in both equations, because you can then use addition or subtraction to cancel one of the variables out, and solve for the other variable.
For this problem, elimination makes the most sense because our 
Next, we can divide both sides by 
Remember, when we are solving a system of linear equations, we are looking for the point of intersection; thus, our answer should have both 

Now that we have the value of 

We want to subtract 
Then divide both sides by 
Our point of intersection, and the solution to the two system of linear equations is
Example Question #171 : Expressions & Equations
Use algebra to solve the following system of linear equations:
There are a couple of ways to solve a system of linear equations: graphically and algebraically. In this lesson, we will review the two ways to solve a system of linear equations algebraically: substitution and elimination.
Substitution can be used by solving one of the equations for either 


Elimination is best used when one of the variables has the same coefficient in both equations, because you can then use addition or subtraction to cancel one of the variables out, and solve for the other variable.
For this problem, elimination makes the most sense because our 
Next, we can divide both sides by 
Remember, when we are solving a system of linear equations, we are looking for the point of intersection; thus, our answer should have both 

Now that we have the value of 

We want to subtract 
Our point of intersection, and the solution to the two system of linear equations is
Certified Tutor
All Common Core: 8th Grade Math Resources




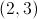








































































![\frac{\begin{array}[b]{r}-7x-y=4\\ +\ 4x+y=-7\end{array}}{ -3x=-3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/953479/gif.latex)







![\frac{\begin{array}[b]{r}4+y=-7\\ \ -4\ \ \ \ \ \ \ \ -4\end{array}}{\\\\y=-11}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/953493/gif.latex)








![\frac{\begin{array}[b]{r}4x-4y=5\\ -\ 9x-4y=-15\end{array}}{ -5x=20}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/953833/gif.latex)




![\frac{\begin{array}[b]{r}-16-4y=5\\ \ +16\ \ \ \ \ \ +16\end{array}}{\\\\-4y=21}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/953840/gif.latex)











![\frac{\begin{array}[b]{r}2x+2y=16\\ -\ 6x+2y=20\end{array}}{ -4x=-4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/953814/gif.latex)



![\frac{\begin{array}[b]{r}2+2y=16\\ \ -2\ \ \ \ \ \ \ \ -2\end{array}}{\\\\2y=14}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/953820/gif.latex)











![\frac{\begin{array}[b]{r}9x+3y=27\\ -\ 4x+3y=12\end{array}}{ 5x=15}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/953776/gif.latex)




![\frac{\begin{array}[b]{r}12+3y=12\\ \ -12\ \ \ \ \ \ \ \ -12\end{array}}{\\\\3y=0}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/953783/gif.latex)











![\frac{\begin{array}[b]{r}-4x+y=20\\ -\ 6x+y=30\end{array}}{ -10x=-10}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/954090/gif.latex)



![\frac{\begin{array}[b]{r}6+y=30\\ \ -6\ \ \ \ \ \ \ \ -6\end{array}}{\\\\y=24}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/954096/gif.latex)




