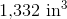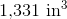All Common Core: 7th Grade Math Resources
Example Questions
Example Question #332 : Isee Upper Level (Grades 9 12) Mathematics Achievement
Give the volume of a cube with surface area 240 square inches.
Let be the length of one edge of the cube. Since its surface area is 240 square inches, one face has one-sixth of this area, or square inches. Therefore, , and .
The volume is the cube of this, or cubic inches.
Example Question #1 : Finding Volume Of A Cube
Calculate the volume of the provided figure.

In order to solve this problem, we need to recall the volume formula for a cube:
Now that we have the correct formula, we can substitute in our known values and solve:
Example Question #31 : Solve Problems Involving Area, Volume And Surface Area Of Two And Three Dimensional Objects: Ccss.Math.Content.7.G.B.6
Calculate the volume of the provided figure.

In order to solve this problem, we need to recall the volume formula for a cube:
Now that we have the correct formula, we can substitute in our known values and solve:
Example Question #31 : Solve Problems Involving Area, Volume And Surface Area Of Two And Three Dimensional Objects: Ccss.Math.Content.7.G.B.6
Calculate the volume of the provided figure.

In order to solve this problem, we need to recall the volume formula for a cube:
Now that we have the correct formula, we can substitute in our known values and solve:
All Common Core: 7th Grade Math Resources