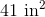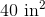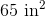All Common Core: 7th Grade Math Resources
Example Questions
Example Question #1 : Solve For Area Of A Rectangle
Calculate the area of the provided figure.

In order to solve this problem, we need to recall the area formula for a rectangle:
Now that we have the correct formula, we can substitute in our known values and solve:
Example Question #1 : Solve Problems Involving Area, Volume And Surface Area Of Two And Three Dimensional Objects: Ccss.Math.Content.7.G.B.6
Calculate the area of the provided figure.

In order to solve this problem, we need to recall the area formula for a rectangle:
Now that we have the correct formula, we can substitute in our known values and solve:
Example Question #1 : Solve For Area Of A Rectangle

In rectangle ABCD, the perimeter is 48 and side BC measures 4. What is the area of rectangle ABCD?
88
48
80
64
72
80
The perimeter of a rectangle is 2L + 2W, or 2 times the length plus 2 times the width. Here you're given that side BC is 4, which means that the opposite side, AD, is also 4. So since that is two widths, you now have:
8 + 2L = 48
So 2L = 40
That means that the length is 20.
Since the area is LW, you can calculate the area as 20 * 4 = 80.
Example Question #1 : Solve For Area Of A Rectangle

What is the area of rectangle WXYZ?
120
50
100
125
150
150
The area of a triangle is Length times Width. Here you can see that the length is 15 and the width is 10, so when you multiply 15 * 10 the answer is 150.
Example Question #1 : Solve For Area Of A Rectangle
A rectangle's length is twice as long as its width. If the width of the rectangle is 4, what is its area?
16
32
8
24
12
32
The area of a rectangle is Length * Width. Here you're given the width as 4, so all you need to do is find the length and you can apply the formula.
Since the width is 4 and you know that the length is twice as long, that makes the length 8. Then Length * Width would be 8 * 4 = 32.
Example Question #914 : Grade 7
A rectangle has sides of 2, 2, 7, and 7. What is the area of that rectangle?
22
9
18
14
7.5
14
The area of a triangle is Length * Width, and in a rectangle opposite sides are parallel and have the same length. So here you know that the widths are 2 and the lengths are 7. So multiply 7 * 2 to get your answer, which is 14.
Example Question #1 : Solve For Area Of A Triangle
Calculate the area of the provided figure.

In order to solve this problem, we need to recall the area formula for a triangle:
Now that we have the correct formula, we can substitute in our known values and solve:
Example Question #912 : Grade 7

What is the area of the triangle pictured above?
40
30
12
60
24
24
The area of a triangle is calculated using the formula 

Example Question #913 : Grade 7

In triangle ABC above, the distance between point A and point D is 10 inches, and the area of the triangle is 20 square inches. What is the length of side BC?
10 inches
There is not enough information to answer the question
4 inches
8 inches
2 inches
4 inches
The area of a triangle can be calculated using the formula Area = 1/2 * Base * Height. Here you're given two of the unknowns in that formula:
Area = 20
Height = 10
So you can plug those into the area formula to solve for Base, the only remaining unknown:
20 = 1/2 * Base * 10
That means that 20 = 5 * Base, so Base = 4.
Example Question #1 : Solve For Area Of A Triangle

In triangle ABC, side BC measures 12 meters, and the shortest straight-line distance between point A and side BC is 5 meters long. What is the area of triangle ABC?
30
36
60
24
12
30
The area of a triangle can be calculated using the formula 
Certified Tutor
Certified Tutor
All Common Core: 7th Grade Math Resources