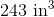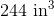All Common Core: 7th Grade Math Resources
Example Questions
Example Question #912 : Grade 7

The pictured right triangle has sides of 7, 24, and 25. What is the area of that triangle?
125
64
84
77
128
84
The area of a triangle can be calculated using the formula 
Example Question #1 : Finding Volume Of A Rectangular Prism
An aquarium is shaped like a perfect cube; the perimeter of each glass face is 

Insufficient information is given to answer the question.
Note:
A perfect cube has square faces; if a face has perimeter 


Its capacity in liters is 


This rounds to
Example Question #2 : Finding Volume Of A Rectangular Prism
Calculate the volume of the provided figure.

In order to solve this problem, we need to recall the volume formula for a rectangular prism:
Now that we have the correct formula, we can substitute in our known values and solve:
Example Question #2 : Finding Volume Of A Rectangular Prism
Calculate the volume of the provided figure.

In order to solve this problem, we need to recall the volume formula for a rectangular prism:
Now that we have the correct formula, we can substitute in our known values and solve:
Example Question #4 : Finding Volume Of A Rectangular Prism
Calculate the volume of the provided figure.

In order to solve this problem, we need to recall the volume formula for a rectangular prism:
Now that we have the correct formula, we can substitute in our known values and solve:
Example Question #1 : How To Find The Volume Of A Prism
A rectangular prism has the following dimensions:
Length:
Width:
Height:
Find the volume.
Given that the dimensions are: 






This final value can be approximated to 
Example Question #3 : How To Find The Volume Of A Prism
Solve for the volume of a prism that is 4m by 3m by 8m.
The volume of the rectangle

so we plug in our values and obtain

Example Question #1 : Finding Volume Of A Rectangular Prism
The dimensions of Treasure Chest A are 39” x 18”. The dimensions of Treasure Chest B are 16” x 45”. Both are 11” high. Which of the following statements is correct?
There is insufficient data to make a comparison between Treasure Chest A and Treasure Chest B.
Treasure Chest B can hold more treasure.
Treasure Chest A can hold more treasure.
Treasure Chest A has the same surface area as Treasure Chest B.
Treasure Chest A and B can hold the same amount of treasure.
Treasure Chest B can hold more treasure.
The volume of B is 7920 in3. The volume of A is 7722 in3. Treasure Chest B can hold more treasure.
Example Question #1 : Finding Volume Of A Rectangular Prism
A rectangular prism has a width of 3 inches, a length of 6 inches, and a height triple its length. Find the volume of the prism.
A rectangular prism has a width of 3 inches, a length of 6 inches, and a height triple its length. Find the volume of the prism.
Find the volume of a rectangular prism via the following:
Where l, w, and h are the length width and height, respectively.
We know our length and width, and we are told that our height is triple the length, so...
Now that we have all our measurements, plug them in and solve:
Example Question #2 : Finding Volume Of A Rectangular Prism

The above diagram shows a rectangular solid. The shaded side is a square. In terms of 
A square has four sides of equal length, as seen in the diagram below.

The volume of the solid is equal to the product of its length, width, and height, as follows:

Certified Tutor
Certified Tutor
All Common Core: 7th Grade Math Resources