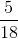Call Now to Set Up Tutoring:

(888) 888-0446

Common Core: 7th Grade Math : Develop and Compare Probability Models and Find Probabilities of Events: CCSS.Math.Content.7.SP.C.7

Study concepts, example questions & explanations for Common Core: 7th Grade Math

Create An Account

All Common Core: 7th Grade Math Resources

7 Diagnostic Tests 110 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #791 : Grade 7

Set consists of the numbers (3,4) . Set n consists of the numbers (5,6) . If a number is randomly selected from set and multiplied by a number randomly selected from set , what is the chance the product will be ?

Possible Answers:

$\frac{2}{3}$

$\frac{1}{4}$

$\frac{1}{2}$

$\frac{1}{3}$

Correct answer:

$\frac{1}{4}$

Explanation:

The only way that a product of will be acheived is if the number is selected from set , and the number is selected from set .

There is a one half chance of the number 4 being selected and a one half chance of the number 6 being selected, given that each set contains two numbers.

Therefore, the probability of both these number being chosen is:

$\frac{1}{2}* \frac{1}{2}=\frac{1}{4}$

Report an Error

Example Question #21 : Develop And Compare Probability Models And Find Probabilities Of Events: Ccss.Math.Content.7.Sp.C.7

If Mark flips a coin and then rolls a die, what are the odds that the coin will be heads and that the die will land on a multiple of 3?

Possible Answers:

$\frac{1}{3}$

$\frac{1}{6}$

$\frac{1}{12}$

$\frac{1}{4}$

Correct answer:

$\frac{1}{6}$

Explanation:

If Mark flips a coin, the chance that it will land on heads is $\frac{1}{2}$ . On a die, there are 2 out of 6 numbers that are a multiple of 3 (3 and 6); therefore, there is a $\frac{1}{3}$ chance that the dice will be a multiple of 3.

The probability that the coin will land on heads and that the dice will be a multiple of 3 is:

$\frac{1}{2}*\frac{1}{3}=\frac{1}{6}$

Report an Error

Example Question #21 : How To Find The Probability Of An Outcome

If Janet rolls a pair of six-sided dice, what is the probability that the dice will come up as snake eyes (meaning that both dice show one dot)?

Possible Answers:

$\frac{1}{36}$

$\frac{1}{12}$

$\frac{1}{6}$

$\frac{1}{3}$

Correct answer:

$\frac{1}{36}$

Explanation:

Given that there are six values that a die may show when rolled, there is a $\frac{1}{6}$ chance that either dice will show a value of 1. Thus, the chance that both dice will show a value of 1 is equal to $\frac{1}{6}* \frac{1}{6}$ , which is equal to $\frac{1}{36}$ .

Thus, $\frac{1}{36}$ is the correct answer.

Report an Error

Example Question #792 : Grade 7

If you are picking a random student from a bus with freshmen, sophomores, juniors, and seniors, what is the probability that you pick a senior?

Possible Answers:

0.21

0.29

0.71

0.26

0.24

Correct answer:

0.29

Explanation:

To find the probability of an event, you divide the possible outcomes of that event by total outcomes.

The event outcomes would be the seniors on the bus.

The total outcomes is the number of students on the bus which is

$42 \left ( 9+10+11+12=42\right )$ .

So the probability of picking a senior would be

$\frac{12}{42}=0.29$ .

Report an Error

Example Question #21 : Develop And Compare Probability Models And Find Probabilities Of Events: Ccss.Math.Content.7.Sp.C.7

What is the probability of drawing a card that is a spade from a deck of cards?

Possible Answers:

$\frac{1}{13}$

$\frac{1}{2}$

$\frac{1}{52}$

$\frac{1}{4}$

Correct answer:

$\frac{1}{4}$

Explanation:

There are cards in a deck.

There are four suits of cards including spades.

They make up an even amount of the deck each.

Since there are four of the suits, each represent $\frac{1}{4}$ of the deck and that is the probability of drawing one.

Report an Error

Example Question #22 : Develop And Compare Probability Models And Find Probabilities Of Events: Ccss.Math.Content.7.Sp.C.7

Find the probability of drawing a 2 from a deck of cards.

Possible Answers:

$\frac{1}{4}$

$\frac{1}{52}$

$\frac{1}{13}$

$\frac{2}{52}$

Correct answer:

$\frac{1}{13}$

Explanation:

To find the probability of an event, we use the following:

$\text{probability of an event} = \frac{\text{number of ways the event can happen}}{\text{number of total possible outcomes}}$

So, when looking at the event of drawing a 2 from a deck of cards, we get

$\text{number of ways the event can happen} = 4$

It is 4 because we can draw a 2 from a deck of cards 4 different ways:

2 of hearts
2 of diamonds
2 of clubs
2 of spades

Now,

$\text{number of total possible outcomes} = 52$

because there are 52 cards in the entire deck. Now,

$\text{probability of drawing a 2} = \frac{4}{52}$

We can simplify, we get

$\frac{4}{52} = \frac{2}{26} = \frac{1}{13}$

Therefore, the probability of drawing a 2 from a deck of cards is $\frac{1}{13}$

Report an Error

Example Question #23 : Develop And Compare Probability Models And Find Probabilities Of Events: Ccss.Math.Content.7.Sp.C.7

Find the probability of drawing a 9 of hearts from a deck of cards.

Possible Answers:

$\frac{1}{13}$

$\frac{1}{4}$

$\frac{1}{52}$

$\frac{2}{52}$

Correct answer:

$\frac{1}{52}$

Explanation:

To find the probability of an event, we use the following:

$\text{probability of an event} = \frac{\text{number of ways the event can happen}}{\text{number of total possible outcomes}}$

So, when looking at the event of drawing a 9 of hearts from a deck of cards, we get

$\text{number of ways the event can happen} = 1$

It is 1 because we can draw a 9 of hearts from a deck of cards in only 1 way:

9 of hearts

Now,

$\text{number of total possible outcomes} = 52$

because there are 52 cards in the entire deck. Now,

$\text{probability of drawing a 9 of hearts} = \frac{1}{52}$

Therefore, the probability of drawing a 2 from a deck of cards is $\frac{1}{52}$

Report an Error

Example Question #794 : Grade 7

At Lisa's school, $52\%$ of her class consists of girls. There are students in her class. On the first day of school, girls wore skirts. How many girls did not wear skirts?

Possible Answers:

Correct answer:

Explanation:

Given that $52\%$ of the class is girls, and there are students, we must first determine how many girls are in the class.

$52\%=\frac{52}{100}$

$\frac{52}{100}=\frac{x}{50}$

Because 100 is double the value of , is double the value of . should be half of .

$\frac{52}{100}=\frac{2\times x}{2\times50}=\frac{2x}{100}$

52=2x

$x=\frac{52}{2}=26$

If of the girls wear skirts, then we can subtract to find the number of girls not wearing skirts.

26-12=14

Report an Error

Example Question #24 : Develop And Compare Probability Models And Find Probabilities Of Events: Ccss.Math.Content.7.Sp.C.7

Billy's mom baked a pizza with eight slices. Half the slices have pepperoni only. Two of the slices have both pepperoni and onions. One slice has onions only. One slice has only cheese.

If Billy is allergic to pepperoni, and takes a slice of pizza with his eyes blindfolded, what is the percentage chance that he will select a piece he is not allergic to?

Possible Answers:

$80\%$

$0\%$

$25\%$

$50\%$

Correct answer:

$25\%$

Explanation:

The pizza that Billy's mom baked was composed of these types of slices:

Half the slices have pepperoni only. Two of the slices have both pepperoni and onoins. One slice has onions only. One slice has only cheese.

Therefore,

slices had pepperoni because $8\div2=4$

slices had pepperoni and onions

slice had onion only

slice had only cheese.

Billy could eat either the onion only slice, or the cheese only slice. This means that out of pieces of pizza, he could eat .

$\frac{2}{8}=\frac{1}{4}$

Given that $25\%$ is the percent equivalent of $\frac{1}{4}$ , that is the correct answer.

Report an Error

Example Question #24 : Outcomes

Two fair dice are thrown. What is the probability that the difference of the numbers that show on the dice will be exactly ?

Possible Answers:

$\frac{5}{18}$

$\frac{7}{18}$

$\frac{1}{4}$

$\frac{1}{3}$

Correct answer:

$\frac{5}{18}$

Explanation:

The following rolls result in the difference of the dice being :

(1,2), (2,3), (3,4), (4,5), (5,6) and the reverse of each of these.

These are rolls out of a possible , so the probability of this event is $\frac{10}{36} = \frac{5}{18}$

Report an Error

View Tutors

Rainier
Certified Tutor

Norfolk State University, Bachelors, Physics.

View Tutors

Marlene
Certified Tutor

Herbert Lehman, Bachelors, Recreation Education. Long Island University-Brooklyn Campus, Masters, Special Education.

View Tutors

Sarah
Certified Tutor

New York University, Bachelor of Fine Arts, Drama.

All Common Core: 7th Grade Math Resources

7 Diagnostic Tests 110 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

English Tutors in Houston, MCAT Tutors in Chicago, SSAT Tutors in San Diego, SSAT Tutors in Phoenix, Statistics Tutors in Phoenix, French Tutors in Philadelphia, Reading Tutors in Dallas Fort Worth, Math Tutors in Los Angeles, SSAT Tutors in Boston, Algebra Tutors in Dallas Fort Worth

Popular Courses & Classes

GMAT Courses & Classes in Los Angeles, ACT Courses & Classes in Washington DC, Spanish Courses & Classes in New York City, ISEE Courses & Classes in San Diego, GMAT Courses & Classes in Denver, LSAT Courses & Classes in New York City, ACT Courses & Classes in Los Angeles, GRE Courses & Classes in Miami, ISEE Courses & Classes in Seattle, SSAT Courses & Classes in Atlanta

Popular Test Prep

SAT Test Prep in Miami, SSAT Test Prep in Chicago, ACT Test Prep in Los Angeles, ISEE Test Prep in Phoenix, ACT Test Prep in Washington DC, MCAT Test Prep in Los Angeles, ISEE Test Prep in Chicago, GMAT Test Prep in Los Angeles, ISEE Test Prep in San Diego, ACT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Common Core: 7th Grade Math : Develop and Compare Probability Models and Find Probabilities of Events: CCSS.Math.Content.7.SP.C.7

Study concepts, example questions & explanations for Common Core: 7th Grade Math

All Common Core: 7th Grade Math Resources

Example Questions

Example Question #791 : Grade 7

Example Question #21 : Develop And Compare Probability Models And Find Probabilities Of Events: Ccss.Math.Content.7.Sp.C.7

Example Question #21 : How To Find The Probability Of An Outcome

Example Question #792 : Grade 7

Example Question #21 : Develop And Compare Probability Models And Find Probabilities Of Events: Ccss.Math.Content.7.Sp.C.7

Example Question #22 : Develop And Compare Probability Models And Find Probabilities Of Events: Ccss.Math.Content.7.Sp.C.7

Example Question #23 : Develop And Compare Probability Models And Find Probabilities Of Events: Ccss.Math.Content.7.Sp.C.7

Example Question #794 : Grade 7

Example Question #24 : Develop And Compare Probability Models And Find Probabilities Of Events: Ccss.Math.Content.7.Sp.C.7

Example Question #24 : Outcomes

All Common Core: 7th Grade Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: