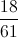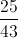The rolls that yield a product between  and  inclusive are:

Therefore there are  rolls that fit our criteria out of a total of  possible rolls, so the probability of this outcome is .

The probability of an event based on observation (empirical probability) can be calculated by dividing the number of times the event occurs by the number of trials total. Since there were  trials and  heads, there were  tails.

The probability of tails is therefore given by the number of tails divided by the total number of trials. Both terms are divisible by , allowing us to simplify the fraction.

There are   possible rolls of two fair six-sided dice, each of which will come up with equal probability. The set of rolls is shown below, with the ways to roll a sum of 8 or 9 indicated.

There are 9 ways out of 36 to roll a sum of 8 or 9, making the probability of this outcome .

To find the probability of an event, we will use the following formula:

So, if we look at the event of drawing a 10 from a deck of cards, we can determine the following:

because there are 4 ways we can draw a 10:

• 10 of hearts
• 10 of diamonds
• 10 of clubs
• 10 of spades

because there are 52 total cards to choose from.  

Knowing all of this, we can substitute into the formula.  We get

Now, we simplify.

Therefore, the probability of drawing a 10 from a deck of cards is .

To find the probability of an event, we will use the following formula:

So, if we look at the event of rolling an even number on a dice, we can determine the following:

because there are 3 ways we can roll an even number on a dice:

• 2
• 4
• 6

because there are 6 possible numbers we can roll:

• 1
• 2
• 3
• 4
• 5
• 6 

Knowing all of this, we can substitute into the formula.  We get

Now, we simplify.

Therefore, the probability of rolling an even number on a dice is .

To find the probability of an event, we use the following formula:

Now, we are asked to find the probability of drawing a 2 from a deck of cards.  Given that event, we can determine

because there are 4 ways to draw a 2 from a deck of cards:

• 2 of hearts
• 2 of diamonds
• 2 of clubs
• 2 of spades

Now, we can determine the total number of possible outcomes

because there are 52 different cards to choose from.

Knowing this, we can substitute into the formula.

Now, we can simplify.

Therefore, the probability of drawing a 2 from a deck of cards is .

To find the probability of an event, we use the following formula:

Now, we are asked to find the probability of drawing an Ace of spades from a deck of cards.  Given that event, we can determine

because there is only 1 Ace of spades in a deck of cards.

Now, we can determine the total number of possible outcomes

because there are 52 different cards to choose from.

Knowing this, we can substitute into the formula.

Therefore, the probability of drawing an Ace of spades from a deck of cards is .

To find the probability of an event, we will use the following formula:

So, given the event of drawing a King from a deck of cards, we can see

because there are 4 Kings in a deck of cards:

1. King of Hearts
2. King of Diamonds
3. King of Clubs
4. King of Spades

Now, we will look at total outcomes.  We get

because there are 52 cards in a deck (in other words 52 different possibilities when drawing a card).

Knowing this, we can substitute into the formula.  We get

Now, we simplify.

Therefore, the probability of drawing a King from a deck of cards is .

To find the probability of an event, we will use the following formula:

So, given the event of drawing a 7 of Diamonds from a deck of cards, we can see

because there is only 1 7 of Diamonds in a deck of cards.

Now, we will look at total outcomes.  We get

because there are 52 cards in a deck (in other words 52 different possibilities when drawing a card).

Knowing this, we can substitute into the formula.  We get

Therefore, the probability of drawing a King from a deck of cards is .

Each number will be represented by one red ball, so there will be ten red balls in the box.

The prime numbers - the numbers that have only 1 and themselves as factors - are 2, 3, 5, and 7, so there will be four green balls.

The composite numbers - the numbers that have more than two factors - are 4, 6, 8, 9, and 10, so there will be five blue balls. 

Note that 1 is neither prime nor composite.

The total number of balls is , four of which are green, so the probability of drawing a green ball at random is .