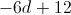All Common Core: 6th Grade Math Resources
Example Questions
Example Question #1 : Apply The Properties Of Operations To Generate Equivalent Expressions: Ccss.Math.Content.6.Ee.A.3
Simplify the following expression:
Apply the distributive property of multiplication to remove the parenthesis from the given expression. Multiply the term outside of the parenthesis to each of the terms inside the parenthesis.
Example Question #14 : Distributive Property
Simplify the following:
This is applying to distrubtive property and then combining like terms.
First you distrubute the negative to the two terms in the first parentheses, so:
Then do the same for the four:
Finally, combine like terms to get:
Example Question #3 : Apply The Properties Of Operations To Generate Equivalent Expressions: Ccss.Math.Content.6.Ee.A.3
Name the property used to solve the problem.
Communitive Property of Multiplication
Associative Property of Multiplication
Multiplication Property
Distributive Property
Identity Property
Distributive Property
Multiplying each term on the outside of the parenthesis by each term on the inside refers to the distributive property.
Example Question #291 : Expressions & Equations
Simplify the following expression using the distributive property.
Distributive property is used to multiply a single term by two or more terms inside a set of parenthesis. Multiply the outside term (5) by 7
Then multiply the outside term (5) by 9.
Combine the two remaining terms by keeping the sign that was originally inside the parenthesis.
Example Question #4 : How To Use The Distributive Property In Pre Algebra
Which of the following is equivalent to 
We need to distribute -3 by multiplying both terms inside the parentheses by -3.:

Now we can multiply and simplify. Remember that multiplying two negative numbers results in a positive number:
Example Question #1 : Distributive Property
Distribute:
Remember that a negative multiplied by a negative is positive, and a negative multiplied by a positive is negative.
Distribute the 
Example Question #412 : Operations And Properties
Solve the equation using the distributive property.
First, we must use the distributive property on both sides of the equation.
The distributive property states:
Therefore:
Now, we can solve the expression like a two-step equation with variables on both sides. Do not forget the properties of equality and perform the same operations on both sides.
Subtract 

Simplify.
Now, the problem is a one-step equation.
Add 

Solve.
Check the answer by substituting it back into the original equation. Both sides should equal to each other.
Example Question #413 : Operations And Properties
Simplify using the distributive property:
First, we must use the distributive property on both sides of the equation.
The distributive property states:
In other words, we can take the factor on the outside of the parentheses and multiply it by each term inside the parentheses.
Therefore:
Simplify.
Example Question #291 : Expressions & Equations
Select the expression that is equal to
To solve this problem we need to use the distributive property. This property is used to multiply a term outside of a set of parentheses by each of the terms in the parentheses.
Now we have
This expression is simplified because we cannot add 



Example Question #742 : Grade 6
Select the expression that is equal to
To solve this problem we need to use the distributive property. This property is used to multiply a term outside of a set of parentheses by each of the terms in the parentheses.
Now we have
This expression is simplified because we cannot add 



All Common Core: 6th Grade Math Resources