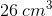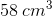We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Common Core: 6th Grade Math : Find the Volume of a Right Rectangular Prism with Fractional Edge Lengths: CCSS.Math.Content.6.G.A.2

Study concepts, example questions & explanations for Common Core: 6th Grade Math

Create An Account

All Common Core: 6th Grade Math Resources

6 Diagnostic Tests 186 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Find The Volume Of A Right Rectangular Prism With Fractional Edge Lengths: Ccss.Math.Content.6.G.A.2

A large crate in the shape of a rectangular prism has dimensions 5 feet by 4 feet by 12 feet. Give its volume in cubic yards.

Possible Answers:

$10 \textrm{ yd}^{3}$

$7 \frac{2}{9 } \textrm{ yd}^{3}$

$90\textrm{ yd}^{3}$

$80 \textrm{ yd}^{3}$

$8 \frac{8}{9 } \textrm{ yd}^{3}$

Correct answer:

$8 \frac{8}{9 } \textrm{ yd}^{3}$

Explanation:

Divide each dimension by 3 to convert feet to yards, then multiply the three dimensions together:

V = LWH

$V = \frac{5}{3} \cdot \frac{4}{3} \cdot \frac{12}{3}$

$V = \frac{5}{3} \cdot \frac{4}{3} \cdot \frac{4}{1}$

$V = \frac{80}{9 } = 8 \frac{8}{9 } \textrm{ yd}^{3}$

Report an Error

Example Question #1 : Prisms

Which is the greater quantity?

(A) The volume of a rectangular solid ten inches by twenty inches by fifteen inches

(B) The volume of a cube with sidelength sixteen inches

Possible Answers:

It is impossible to determine which is greater from the information given

(A) is greater

(A) and (B) are equal

(B) is greater

Correct answer:

(B) is greater

Explanation:

The volume of a rectangular solid ten inches by twenty inches by fifteen inches is

$V = 10 \cdot 20 \cdot15 = 3,000$ cubic inches.

The volume of a cube with sidelength 13 inches is

$V = 16^{3} = 16 \cdot 16 \cdot 16 = 4,096$ cubic inches.

This makes (B) greater

Report an Error

Example Question #2 : Find The Volume Of A Right Rectangular Prism With Fractional Edge Lengths: Ccss.Math.Content.6.G.A.2

A prism with a square base has a height of feet.

If the edge of the base is feet, what is the volume of the prism?

Possible Answers:

$8\, ft^3$

$16\, ft^3$

$4\, ft^3$

$6\, ft^3$

Correct answer:

$16\, ft^3$

Explanation:

The volume of a prism is given as

V = Bh

where

B = Area of the base

and

h = height of the prism.

Because the base is a square, we have

B = s^2 = 2^2 = 4

So plugging in the value of B that we found and h that was given in the problem we get the volume to be the following.

$V = 4\cdot4 = 16\,ft^3$

Report an Error

Example Question #2 : Find The Volume Of A Right Rectangular Prism With Fractional Edge Lengths: Ccss.Math.Content.6.G.A.2

A rectangular prism has the dimensions of $2\:in$ , $5\:in$ , and $7\:in$ . What is the volume of the prism?

Possible Answers:

$70\:in^2$

$72\:in^3$

$63 \:in^2$

$63\: in^3$

$70\:in^3$

Correct answer:

$70\:in^3$

Explanation:

The volume of a rectangular prism is given by the following equation:

$V= l \cdot w \cdot h$

In this equation, is length, is width, and is height.

The given information does not explicitly state which side each dimension measurement correlates to on the prism. Volume simply requires the multiplication of the dimensions together.

Volume can be solved for in the following way:

$V = 2\:in \cdot 5\:in \cdot 7\:in$

$V = 10\:in^2 \cdot 7\:in$

$V= 70 \:in^3$

Report an Error

Example Question #3 : Find The Volume Of A Right Rectangular Prism With Fractional Edge Lengths: Ccss.Math.Content.6.G.A.2

Find the volume of a rectangular prism with a width of $2\:cm$ , height of $8\:cm$ and length of $3\:cm$ .

Possible Answers:

$48\:cm^3$

$58\:cm^3$

$26\:cm^3$

$24\:cm^3$

$56\:cm^3$

Correct answer:

$48\:cm^3$

Explanation:

The volume of a rectangular prism is given by the following equation:

$V= l \cdot w \cdot h$

In this equation, is length, is width, and is height.

Because all the necessary information has been provided to solve for the volume, all that needs to be done is substituting in the values for the variables.

Therefore:

$V = 2\:cm \cdot 3\:cm \cdot 8\:cm$

$V = 6\:cm^2 \cdot 8\:cm$

$V = 48\:cm^3$

Report an Error

Example Question #3 : Find The Volume Of A Right Rectangular Prism With Fractional Edge Lengths: Ccss.Math.Content.6.G.A.2

Find the surface area of the rectangular prism:

Volume_of_a_prism

Possible Answers:

$453\:units^3$

$418\:units^3$

$468\:units^3$

$468\:units^2$

$410\:units^2$

Correct answer:

$410\:units^2$

Explanation:

The surface area of a rectangular prism is

SA=2lw+2lh+2wh

Substituting in the given information for this particular rectangular prism.

$\\SA=2(13\cdot 9)+2(13\cdot 4)+2(9\cdot 4) \\SA=410\ \text{units}^2$

Report an Error

Example Question #4 : Find The Volume Of A Right Rectangular Prism With Fractional Edge Lengths: Ccss.Math.Content.6.G.A.2

A small rectangular fish tank has sides that are 18in wide, 30in long, and 24in high. Which formula would not work to find the correct volume of the fish tank?

Possible Answers:

$(24 \times 18) \times 30$

$(18 \times 30) + 24$

$(30 \times 24) \times 18$

$30 \times 432$

$720 \times 18$

Correct answer:

$(18 \times 30) + 24$

Explanation:

In this question the formula that uses addition will not yield the correct volume of the fish tank:

(18 x 30) + 24

This is the correct answer because in order to find the volume of any rectangular prism one needs to multiply the prism's length, width, and height together.

The volume of a rectangular prism is given by the following equation:

$V= l \cdot w \cdot h$

In this equation, is length, is width, and is height.

To restate, (18 x 30) + 24 is the correct answer because it will NOT yield the correct volume, you would need to multiply by the product of and , not add.

Report an Error

Example Question #8 : Find The Volume Of A Right Rectangular Prism With Fractional Edge Lengths: Ccss.Math.Content.6.G.A.2

What is the volume of the rectangular prism in the following figure?

Possible Answers:

$166\textup{ cm}^3$

$159\textup{ cm}^3$

$160.5\textup{ cm}^3$

$156\textup{ cm}^3$

$158.5\textup{ cm}^3$

Correct answer:

$156\textup{ cm}^3$

Explanation:

The formula used to find volume of a rectangular prism is as follows:

$A=l\times w\times h$

Substitute our side lengths:

$A=6\frac{1}{2}\times3\times8$

$A=156\textup{ cm}^3$

Remember, volume is always written with cubic units because volume is how many cubic units can fit inside of a figure.

Report an Error

Example Question #4 : Find The Volume Of A Right Rectangular Prism With Fractional Edge Lengths: Ccss.Math.Content.6.G.A.2

What is the volume of the rectangular prism in the following figure?

Possible Answers:

$147.5\textup{ cm}^3$

$140\textup{ cm}^3$

$138.5\textup{ cm}^3$

$142\textup{ cm}^3$

$136.5\textup{ cm}^3$

Correct answer:

$136.5\textup{ cm}^3$

Explanation:

The formula used to find volume of a rectangular prism is as follows:

$A=l\times w\times h$

Substitute our side lengths:

$A=6\frac{1}{2}\times3\times7$

$A=136.5\textup{ cm}^3$

Remember, volume is always written with cubic units because volume is how many cubic units can fit inside of a figure.

Report an Error

Example Question #1 : Find The Volume Of A Right Rectangular Prism With Fractional Edge Lengths: Ccss.Math.Content.6.G.A.2

What is the volume of the rectangular prism in the following figure?

Possible Answers:

$180\textup{ cm}^3$

$175.5\textup{ cm}^3$

$185.5\textup{ cm}^3$

$183\textup{ cm}^3$

$190\textup{ cm}^3$

Correct answer:

$175.5\textup{ cm}^3$

Explanation:

The formula used to find volume of a rectangular prism is as follows:

$A=l\times w\times h$

Substitute our side lengths:

$A=6\frac{1}{2}\times3\times9$

$A=175.5\textup{ cm}^3$

Remember, volume is always written with cubic units because volume is how many cubic units can fit inside of a figure.

Report an Error

View Tutors

Sarah
Certified Tutor

New York University, Bachelor of Fine Arts, Drama.

View Tutors

David
Certified Tutor

Kent State University, Bachelors, Marketing. Kent State University at Kent, Masters in Education, Special Education.

View Tutors

Rainier
Certified Tutor

Norfolk State University, Bachelors, Physics.

All Common Core: 6th Grade Math Resources

6 Diagnostic Tests 186 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Physics Tutors in Los Angeles, SAT Tutors in San Francisco-Bay Area, Computer Science Tutors in Houston, Algebra Tutors in Miami, ISEE Tutors in Los Angeles, ACT Tutors in Houston, Reading Tutors in Phoenix, Reading Tutors in Atlanta, GRE Tutors in Los Angeles, Calculus Tutors in Philadelphia

Popular Courses & Classes

ISEE Courses & Classes in Washington DC, MCAT Courses & Classes in Atlanta, Spanish Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Boston, ISEE Courses & Classes in New York City, ACT Courses & Classes in Denver, GRE Courses & Classes in Los Angeles, ISEE Courses & Classes in Miami, SSAT Courses & Classes in Atlanta, ACT Courses & Classes in San Diego

Popular Test Prep

ISEE Test Prep in Houston, LSAT Test Prep in Los Angeles, SAT Test Prep in Chicago, GMAT Test Prep in Boston, ISEE Test Prep in Philadelphia, LSAT Test Prep in Miami, ISEE Test Prep in San Francisco-Bay Area, LSAT Test Prep in Houston, GMAT Test Prep in San Francisco-Bay Area, MCAT Test Prep in San Diego

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Common Core: 6th Grade Math : Find the Volume of a Right Rectangular Prism with Fractional Edge Lengths: CCSS.Math.Content.6.G.A.2

Study concepts, example questions & explanations for Common Core: 6th Grade Math

All Common Core: 6th Grade Math Resources

Example Questions

Example Question #1 : Find The Volume Of A Right Rectangular Prism With Fractional Edge Lengths: Ccss.Math.Content.6.G.A.2

Example Question #1 : Prisms

Example Question #2 : Find The Volume Of A Right Rectangular Prism With Fractional Edge Lengths: Ccss.Math.Content.6.G.A.2

Example Question #2 : Find The Volume Of A Right Rectangular Prism With Fractional Edge Lengths: Ccss.Math.Content.6.G.A.2

Example Question #3 : Find The Volume Of A Right Rectangular Prism With Fractional Edge Lengths: Ccss.Math.Content.6.G.A.2

Example Question #3 : Find The Volume Of A Right Rectangular Prism With Fractional Edge Lengths: Ccss.Math.Content.6.G.A.2

Example Question #4 : Find The Volume Of A Right Rectangular Prism With Fractional Edge Lengths: Ccss.Math.Content.6.G.A.2

Example Question #8 : Find The Volume Of A Right Rectangular Prism With Fractional Edge Lengths: Ccss.Math.Content.6.G.A.2

Example Question #4 : Find The Volume Of A Right Rectangular Prism With Fractional Edge Lengths: Ccss.Math.Content.6.G.A.2

Example Question #1 : Find The Volume Of A Right Rectangular Prism With Fractional Edge Lengths: Ccss.Math.Content.6.G.A.2

All Common Core: 6th Grade Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: