The first step when multiplying decimals is lining up the digits on the right-side regardless of place value. It is okay for a tenths place to be in line with a ones place, we want the numbers lined up on the right. 

Then, multiply the digits furthest to the right. In this case, it would be . The  is placed under the problem in the product's area and the  is carried to the top of the problem above the next set of digits. 

Now we will continue multiplying using the  until we have exhausted all digits in the first row. Next is  we must add the  we carried to the top to our product. . Place the  in the product's area and carry the . 

Multiply  and add the  on top . We will place the  underneath in the product's area. 

You will notice that we have not placed the decimal, that will come at the end of the solution.

The last step in a decimal multiplication problem is to place the decimal. Count how many digits are behind the decimal in your problem and we will do the same in the product. This problem has  digits behind the decimal as you can see in pink. 

We will place the decimal in the product so that there are  digits behind it. Giving us a final answer of 

The first step when multiplying decimals is lining up the digits on the right-side regardless of place value. It is okay for a tenths place to be in line with a ones place, we want the numbers lined up on the right. 

Then, multiply the digits furthest to the right. In this case, it would be . The  is placed under the problem in the product's area. 

Now we will continue multiplying using the  until we have exhausted all digits in the first row. Next is . Place the  in the product's area. There are no more digits to multiply so we don't need to carry any digits to the next place value. 

You will notice that we have not placed the decimal, that will come at the end of the solution.

The last step in a decimal multiplication problem is to place the decimal. Count how many digits are behind the decimal in your problem and we will do the same in the product. This problem has  digits behind the decimal as you can see in pink. 

We will place the decimal in the product so that there are  digits behind it. Giving us a final answer of 

The first step when multiplying decimals is lining up the digits on the right-side regardless of place value. It is okay for a tenths place to be in line with a ones place, we want the numbers lined up on the right. 

Then, multiply the digits furthest to the right. In this case, it would be . The  is placed under the problem in the product's area. 

Now we will continue multiplying using the  until we have exhausted all digits in the first row. Next is . Place the  in the product's area. 

Finally, multiply . There are no more digits to multiply so we place the entire  in the product's area. 

You will notice that we have not placed the decimal, that will come at the end of the solution.

The last step in a decimal multiplication problem is to place the decimal. Count how many digits are behind the decimal in your problem and we will do the same in the product. This problem has  digits behind the decimal as you can see in pink. 

We will place the decimal in the product so that there are  digits behind it. Giving us a final answer of 

The first step when multiplying decimals is lining up the digits on the right-side regardless of place value. It is okay for a tenths place to be in line with a ones place, we want the numbers lined up on the right. 

Then, multiply the digits furthest to the right. In this case, it would be . The  is placed under the problem in the product's area. 

Now we will continue multiplying using the  until we have exhausted all digits in the first row. Next is . Place the  in the product's area. 

Multiply  . We will place the  underneath in the product's area because there are no more digits to multiply in the top row. 

You will notice that we have not placed the decimal, that will come at the end of the solution. Now we can cross out the digits we have exhausted and put a placeholder zero in the product's area to hold the place of the furthest right digit that we have finished with. 

It is time to multiply by our final digit,  in , we start back with the furthest right-hand digit, . . Place the  in the products area and carry the  above the next digit we will multiply. 

Continue multiplying, .  Add the  to the  and place the sum of  in the product's area. 

Finally, we are at the last multiplication step before we combine our product.  . The  is placed in the product's area and we are out of digits to multiply. 

Now we add our partial products together. 

The last step in a decimal multiplication problem is to place the decimal. Count how many digits are behind the decimal in your problem and we will do the same in the product. This problem has  digits behind the decimal as you can see in pink. 

We will place the decimal in the product so that there are  digits behind it. Giving us a final answer of 

The first step when multiplying decimals is lining up the digits on the right-side regardless of place value. It is okay for a tenths place to be in line with a ones place, we want the numbers lined up on the right. 

Then, multiply the digits furthest to the right. In this case, it would be . The  is placed under the problem in the product's area and the  is carried above the next digit. 

Now we will continue multiplying using the  until we have exhausted all digits in the first row. Next is . Add the  to  for a total sum of . The  is placed in the product area since there are no more numbers to multiply. 

You will notice that we have not placed the decimal, that will come at the end of the solution.

The last step in a decimal multiplication problem is to place the decimal. Count how many digits are behind the decimal in your problem and we will do the same in the product. This problem has  digits behind the decimal as you can see in green. 

We will place the decimal in the product so that there are  digits behind it. Giving us a final answer of 

The first step when multiplying decimals is lining up the digits on the right-side regardless of place value. It is okay for a tenths place to be in line with a ones place, we want the numbers lined up on the right. 

Then, multiply the digits furthest to the right. In this case, we only have two digits. . The  is placed under the problem in the product's area because there are no other digits to multiply. 

You will notice that we have not placed the decimal, that will come at the end of the solution.

The last step in a decimal multiplication problem is to place the decimal. Count how many digits are behind the decimal in your problem and we will do the same in the product. This problem has  digits behind the decimal as you can see in green. 

We will place the decimal in the product so that there are  digits behind it. Giving us a final answer of 

When we multiply decimals, we can first think of the problem as regular numbers: . In this problem, we have 2 numbers after each decimal, thus our answer has to have two numbers after the decimal point, so we add a zero as a place holder:

We start counting out the two-place values needed to the right of the . As you can see, the decimal moves from the right of the , to the left of the , and then finally moves another place value to the left of the  and we fill it in with a zero. The image below shows the movement.

We can use base ten blocks to help us solve this problem. Let's review what our base ten blocks are by using a whole number 

When we put this together, we add:

To use base ten blocks to add decimal numbers, we need to think of the base ten blocks a little differently. We think of the hundreds block as one whole. The tens block as tenths because you would need ten of these to make one whole. Finally, the ones block as hundredths because you would need a hundred of these to make one whole: 

Let's look at this problem:

First, we want to represent the  with four tenths blocks and five hundredths blocks: 

Next, we want to take away , which means taking away one of the tenths and one of the hundredths:

We can see that we now have three tenths blocks and four hundredths blocks, which means our answer is 

We can use base ten blocks to help us solve this problem. Let's review what our base ten blocks are by using a whole number 

When we put this together, we add:

To use base ten blocks to add decimal numbers, we need to think of the base ten blocks a little differently. We think of the hundreds block as one whole. The tens block as tenths because you would need ten of these to make one whole. Finally, the ones block as hundredths because you would need a hundred of these to make one whole: 

Let's look at this problem:

First, we want to represent the  with five tenths blocks and six hundredths blocks: 

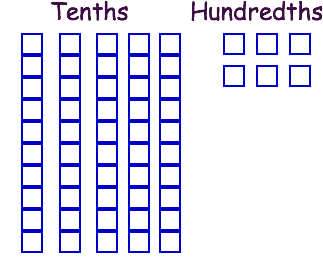
Next, we want to take away , which means taking away three of the tenths and five of the hundredths:

We can see that we now have two tenths blocks and one hundredths block, which means our answer is 

Subtracting decimals is just like subtracting regular numbers. But, you must remember your decimal in your answer: