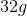All Common Core: 3rd Grade Math Resources
Example Questions
Example Question #101 : Tell And Write Time To The Nearest Minute And Solve Word Problems Involving Time: Ccss.Math.Content.3.Md.A.1
Sam leaves for work at 


For this problem we are subtracting to find a previous time.
We can subtract 



![\frac{\begin{array}[b]{r}4\\ -\ 3\end{array}}{ \ \ \ \space1}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/756925/gif.latex)
He starts to get ready to leave at
Example Question #101 : Measurement And Estimation
Ben leaves for work at 


For this problem we are subtracting to find a previous time.
We can subtract 



![\frac{\begin{array}[b]{r}7\\ -\ 2\end{array}}{ \ \ \ \space5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/756955/gif.latex)
He starts to get ready to leave at
Example Question #103 : Tell And Write Time To The Nearest Minute And Solve Word Problems Involving Time: Ccss.Math.Content.3.Md.A.1
Tanner leaves for work at 


For this problem we are subtracting to find a previous time.
We can subtract 



![\frac{\begin{array}[b]{r}7\\ -\ 2\end{array}}{ \ \ \ \space5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/756965/gif.latex)
He starts to get ready to leave at
Example Question #104 : Measurement & Data
Will leaves for work at 


For this problem we are subtracting to find a previous time.
We can subtract 



![\frac{\begin{array}[b]{r}7\\ -\ 2\end{array}}{ \ \ \ \space5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/756945/gif.latex)
He starts to get ready to leave at
Example Question #105 : Measurement & Data
Jeff leaves for work at 


For this problem we are subtracting to find a previous time.
We can subtract 



![\frac{\begin{array}[b]{r}7\\ -\ 2\end{array}}{ \ \ \ \space5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/756867/gif.latex)
He starts to get ready to leave at
Example Question #106 : Measurement & Data
Scott leaves for work at 


For this problem we are subtracting to find a previous time.
We can subtract 



![\frac{\begin{array}[b]{r}7\\ -\ 2\end{array}}{ \ \ \ \space5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/756915/gif.latex)
He starts to get ready to leave at
Example Question #107 : Measurement & Data
Chuck leaves for work at 


For this problem we are subtracting to find a previous time.
We can subtract 



![\frac{\begin{array}[b]{r}7\\ -\ 2\end{array}}{ \ \ \ \space5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/756904/gif.latex)
He starts to get ready to leave at
Example Question #101 : Measurement And Estimation
When Matt got home from school he immediately started watching a television show. He watched the show for 


For this problem we are subtracting to find a previous time.
We can subtract 



![\frac{\begin{array}[b]{r}8\\ -\ 2\end{array}}{ \ \ \ \space6}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/754694/gif.latex)
He started watching the television show at
Example Question #101 : Measurement & Data
Megan is working on a science experiment. Using the scale below, how much water will she have if she adds 

Megan has 

Example Question #2 : Measure Volume And Solve One Step Word Problems Involving Volume: Ccss.Math.Content.3.Md.A.2
Megan is working on a science experiment. Using the scale below, how much water will she have if she adds 

Megan has 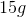

All Common Core: 3rd Grade Math Resources






![\frac{\begin{array}[b]{r}30\\ -\ 15\end{array}}{ \ \ \ \space 15}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/756926/gif.latex)






![\frac{\begin{array}[b]{r}16\\ -\ 10\end{array}}{ \ \ \ \ \ \space 6}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/756956/gif.latex)






![\frac{\begin{array}[b]{r}25\\ -\ 15\end{array}}{ \ \ \ \space 10}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/756966/gif.latex)






![\frac{\begin{array}[b]{r}50\\ -\ 30\end{array}}{ \ \ \ \space 20}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/756946/gif.latex)






![\frac{\begin{array}[b]{r}5\\ -\ 5\end{array}}{ \ \ \ \ \space 0}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/756868/gif.latex)






![\frac{\begin{array}[b]{r}35\\ -\ 20\end{array}}{ \ \ \ \space 15}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/756916/gif.latex)






![\frac{\begin{array}[b]{r}55\\ -\ 42\end{array}}{ \ \ \ \space 13}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/756905/gif.latex)






![\frac{\begin{array}[b]{r}58\\ -\ 50\end{array}}{ \ \ \ \space 8}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/754695/gif.latex)