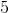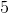All Common Core: 3rd Grade Math Resources
Example Questions
Example Question #23 : Solving Problems Involving The Four Operations, And Identifying And Explaining Patterns In Arithmetic
What is the pattern for the numbers in the X column to the numbers in the Y column?

Add
Divide
Add
Multiply
Subtract
Multiply
Each X value is multiplied by 
To find the rule, you may have to do some trial and error. The most important thing to remember is, once you think you have the rule, make sure to test the rule with all of the X values.
Example Question #791 : Operations & Algebraic Thinking
What is the pattern for the numbers in the X column to the numbers in the Y column?

Add
Add
Add
Multiply
Multiply
Multiply
Each X value is multiplied by 
To find the rule, you may have to do some trial and error. The most important thing to remember is, once you think you have the rule, make sure to test the rule with all of the X values.
Example Question #792 : Operations & Algebraic Thinking
What is the pattern for the numbers in the X column to the numbers in the Y column?

Multiply
Multiply
Add
Multiply
Add
Multiply
Each X value is multiplied by 
To find the rule, you may have to do some trial and error. The most important thing to remember is, once you think you have the rule, make sure to test the rule with all of the X values.
Example Question #26 : Solving Problems Involving The Four Operations, And Identifying And Explaining Patterns In Arithmetic
What is the pattern for the numbers in the X column to the numbers in the Y column?

Multiply
Multiply
Add
Add
Subtract
Multiply
Each X value is multiplied by 
To find the rule, you may have to do some trial and error. The most important thing to remember is, once you think you have the rule, make sure to test the rule with all of the X values.
Example Question #22 : Solving Problems Involving The Four Operations, And Identifying And Explaining Patterns In Arithmetic
What is the pattern for the numbers in the X column to the numbers in the Y column?

Multiply
Add
Multiply
Divide
Add
Multiply
Each X value is multiplied by 
To find the rule, you may have to do some trial and error. The most important thing to remember is, once you think you have the rule, make sure to test the rule with all of the X values.
Example Question #21 : Solving Problems Involving The Four Operations, And Identifying And Explaining Patterns In Arithmetic
Fill in the missing number that completes the sequence:
1, 5, _____, 13
9
25
8
4
9
The first step in solving this problem is identifying the pattern used to create the sequence. It could be any of the four operations (addition, subtraction, multiplication, or division).
The first thing that may be noticed is that the numbers are increasing, which would likely mean the pattern is using addition or multiplication because this leads to larger numbers in the answer rather than smaller answers.
Let's focus on multiplication first, 1x____=5 would be the first step to see if multiplication is the pattern being used. 1x5=5, so this could be our pattern. We must try the rule again with the next digit to see if it follows in sequence. 5x5=25, which is larger than the last number (13) in the series, so multiplication is not the operation used. We can eliminate multiplication.
This leaves us with addition. 1+___=5 reveals that 4 can be added to make 5. To see if the pattern holds, we can try it with 5+4=9 and then use the sum from the attempted pattern to try and make 13. 9+4=13, so we see that 4 works again. This means that the rule is to add each number by 4 to reveal the next number in the sequence.
The missing number in the sequence is 9.
Example Question #22 : Solving Problems Involving The Four Operations, And Identifying And Explaining Patterns In Arithmetic
Fill in the missing number that completes the sequence:
16, 12, 8, ______
6
3
2
4
4
The first step in solving this problem is identifying the pattern used to create the sequence. It could be any of the four operations (addition, subtraction, multiplication, or division).
The first thing that may be noticed is that the numbers are decreasing, which would likely mean the pattern is using subtraction or division because this leads to smaller numbers in the answer rather than larger answers.
Let's focus on division first, 16÷____=12 would be the first step to see if division is the pattern being used. There is no whole number that would give 12 as the quotient to this problem, so with that, we can eliminate division.
This leaves us with subtraction. 16-___=12 reveals that 4 can be subtracted to make 12. To see if the pattern holds, we can try it with 12-___=8 and 4 works again. This means that the rule is to subtract each number by 4 to reveal the next number in the sequence.
8-4=4 so the missing number in the sequence is 4.
Example Question #23 : Solving Problems Involving The Four Operations, And Identifying And Explaining Patterns In Arithmetic
What is the pattern used to create this numerical sequence?
500, 100, 20, 4
Add 80
Subtract by 400
Multiply by 5
Divide by 5
Divide by 5
The first step in solving this problem is identifying the pattern used to create the sequence. It could be any of the four operations (addition, subtraction, multiplication, or division).
Something that may be noticed is that the numbers are decreasing, which would likely mean the pattern is using subtraction or division because this leads to smaller numbers in the answer rather than larger solutions.
Let’s focus on subtraction first, 500-____=100 would be the way to identify the difference between the two numbers and a possible rule. 500-400=100, so the next term would need to be subtracted by 400 to make this rule accurate. 100-400 is NOT 20, so subtraction cannot be the pattern.
This leaves us with division. 500÷___=100 reveals that 5 can be inserted into the blank to make 100. 500÷5=100 is true. To see if the pattern holds, we can try it with 100÷5=20, and it works again. The final test is with the last number in the sequence, 20÷5=4, so the rule holds. Dividing by 5 will get the next term in the series.
The rule is to divide each term by 5.
Example Question #82 : How To Find The Part From The Whole
What is 
When we round a number to the hundreds place we look to our tens place to tell us if we round up or down. If the number in our tens place is 




In this case, 

Example Question #1 : Round Numbers To The Nearest Ten Or Hundred: Ccss.Math.Content.3.Nbt.A.1
What is 
When we round a number to the hundreds place we look to our tens place to tell us if we round up or down. If the number in our tens place is 




In this case, 


All Common Core: 3rd Grade Math Resources