All College Algebra Resources
Example Questions
Example Question #11 : Linear Inequalities
Marvin's Movers charges $100 plus $30 per hour to move a household across town. Elliot's Moving Service charges $55 per hour. For what lengths of time does it cost less to hire Marvin's Movers?
More than 5 hours
Less than 4 hours
More than 6 hours
More than 4 hours
Less than 5 hours
More than 4 hours
Our variable x represents the number of hours to move. Marvin's rate can be expressed as 30x+100. Elliot's rate can be expressed as 55x. We must set the expression for Marvin's rate less than Elliot's rate: 
Example Question #72 : Solving Equations And Inequallities
When is the inequality 
this inequality cannot be satisfied.
We can rewrite this as 


When is this true? When both linear factors are positive, and also when they are both negative.
If we match them up then we do get that the inequality is satisfied when 

Example Question #1 : Polynomial Inequalities
Give the solution set of the inequality
The set of all real numbers
The boundaries of the intervals in the solution set of the polynomial inequality
are the zeroes of the equation
By the Zero Product Property, either

in which case

or

in which case




in the original inequality, and determine whether it is true.

False - do not include

True - include

True - include
Also, the boundary values themselves should not be included, because the inequality symbol 
The solution set is therefore
Example Question #1 : Polynomial Inequalities
Give the solution set of the inequality
The boundaries of the intervals in the solution set of the polynomial inequality
are the zeroes of the equation
By the Zero Product Property, either

in which case

or

in which case




in the original inequality, and determine whether it is true.

False - do not include

False - do not include

True - include
Also, the boundary values themselves should be included, because the inequality symbol 
The solution set is therefore 
Example Question #1 : Polynomial Inequalities
Give the solution set of the inequality
To solve the polynomial inequality
it is necessary to get it into standard form by writing all terms at the same side. Subtract 
The values of 

Factor the polynomial by grouping and taking out the GCFs:
The polynomial cannot be factored further, as 
in which case
or

which has no real solution.
Therefore, the only boundary of the intervals is 7, which divides the real numbers into two intervals, 



False - do not include

True - include
Also, since the inequality symbol 

Example Question #1 : Polynomial Inequalities
Give the solution set of the inequality
To solve the polynomial inequality
it is necessary to get it into standard form by writing all terms at the same side. Subtract 
The values of 

Factor the polynomial by grouping and taking out the GCFs:

By the Zero Factor Property, one of the binomials is equal to 0, so
in which case

in which case

or
in which case









True - include

False - do not include

True - include

False - do not include
Also, the boundary values themselves should not be included, because the inequality symbol 
The solution set is
Example Question #72 : Solving Equations And Inequallities
Which is correct graph of the following function?
None of the other graphs.
First graph
Since the inequality is 
Shade the area outside of the parabola since it is a negative parabola, but greater than or equal to.
Example Question #72 : Solving Equations And Inequallities
Solve
First we substract 
Now we can factor the left hand side
From this, we can see that the roots are at 

To make this inequality true, we will have two answers.
Example Question #73 : Solving Equations And Inequallities
Solve
In order to solve this, we need to figure out what values of x makes the numerator and denominator equal zero.
These values are 

Then test a few numbers greater or lesser than the above values to figure out what range of values make the inequality true.
Example Question #2 : Rational Inequalities
Give the solution set of the equation
The boundary points of a rational inequality are the zeroes of the numerator and the denominator.
First, set the numerator equal to 0 and solve for 
Now set the denominator equal to 0 and solve for 
Factor the trinomial using the reverse-FOIL method. Look for two integers whose sum is 


Set each factor to zero and solve for 
Therefore, the boundary points are 

The four intervals are listed below, along with their arbitrary test points.

True; include 

False; exclude 


True; include


False; exclude 
Since the inequality symbol is the "is greater than or equal to" symbol, include the zero, 0, of the numerator - but not the other two boundaries, the zeroes of the denominator. This makes the solution set
![(-\infty, 0] \cup (1,7)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/970383/gif.latex)
Certified Tutor
Certified Tutor
All College Algebra Resources























































































































































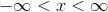













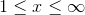
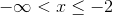


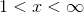





![(-\infty, 0] \cup [1,7]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/970293/gif.latex)
![(-\infty, 0] \cup (1,7)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/970292/gif.latex)


![[0,1]\cup [7, \infty)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/970294/gif.latex)
































