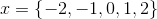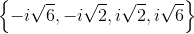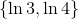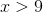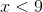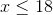Find the roots of the polynomial, 

Set   equal to 

Factor out , 

Notice that the the factor  is a quadratic even though it might not seem so at first glance. One way to think of this is as follows: 

Let 

Then we have ,  substitute into  to get, 

Notice that the change in variable from  to  has resulted in a quadratic equation that can be easily factored due to the fact that it is a square of a simple binomial: 

The solution for  is, 

Because  we go back to the variable , 

Therefore, the roots of the   factor are, 

The other root of  is  since the function clearly equals  when . 

The solution set is therefore, 

Below is a plot of . You can see where the function intersects the -axis at points corresponding to our solutions. 

Further Discussion 

The change of variable was a tool we used to write the quadratic factor in a more familiar form, but we could have just factored the original function in terms of  as follows, 

Setting this to zero gives the same solution set, 

can be rewritten in quadratic form by setting , and, consequently, ; the resulting equation is as follows:

By the reverse-FOIL method we can factor the trinomial at left. We are looking for two integers with sum 8 and product 12; they are 2 and 6, so the equation becomes

Setting both binomials equal to 0, it follows that 

 or .

Substituting  for , we get

 ,

in which case

,

or 

in which case

.

The solution set is .

can be rewritten in quadratic form by setting , and, consequently, ; the resulting equation is as follows:

By the reverse-FOIL method we can factor the trinomial at left. We are looking for two integers with sum 8 and product 12; they are  and , so the equation becomes

Setting both binomials equal to 0, it follows that 

 or .

Substituting  for , we get 

in which case

,

and 

,

in which case 

The set of real solutions is therefore .

Solve for , 

First isolate one of the radicals; the easiest would be the one with more than one term. 

Square both sides of the equation, 

Expand the right side, 

Now collect terms and isolate the remaining radical expression; note the the 's on the left are right sides cancel. 

Square both sides, 

CHECK THE SOLUTION

We have done all of the algebra correctly, but we can still end up with an erroneous solution due to the squaring operation (a very similar problem arises when dealing with absolute value equations). Once you arrive at a solution, make sure you check that the solution works. If it does not work, and you know your algebra was right, then there are no real solutions.

Therefore there are no real solutions. 

using the quadratic formula we get

so the possible solutions are  and . However,  is not an actual solution because it is negative and the equation  can only be satisfied by a positive value.

Square both sides to eliminate the radical.

Divide by three on both sides to isolate the x.

The answer is:  

Square both sides.

Add 2 on both sides.

Divide by 3 on both sides.

The answer is:  

First, isolate the radical on one side of the equation. Start by adding  to both sides of the equation. 

 Now, square both sides of the equation.

Expand the right side of the equation.

Collect all the terms to one side of the equation and simplify to create a quadratic equation equal to zero.

Quadratic equations can be written in the following generic form:

We need to find two numbers whose product equals a multiplied by c and whose sum equals b; therefore, the product of the factors must be -12 and their sum must equal -1. Notice the following:

Write the two quantities. When c is negative, one quantity needs to have a plus sign and one needs to have a minus sign. When b is negative, the larger number should be associated with the minus sign. Write the following quadratic factorization:

The solutions for this quadratic are: 

One common mistake for students is to assume that these solutions are—in fact—solutions to the original equation. Whenever you work with absolute value equations, or radical equations, you must check the solution carefully to make sure the solution actually works. As you will see, only one of the two solutions above actually works in this particular case.

We started with the following equation: 

Now, substitute the solution  into the equation.

We can see that -3 is not a solution. Now, substitute the solution  into the equation.

The correct answer is 4.  

To solve this inequality, we treat is a a regular equation. First, we add 8 to both sides.

.

We now divide both sides by 2 to get 

.

To evaluate, we will need to multiply both sides by one-fifth.

The sign does not need to be switched unless we multiply or divide by a negative value.

The answer is: