College Algebra : College Algebra
Study concepts, example questions & explanations for College Algebra
All College Algebra Resources
Example Questions
Example Question #71 : College Algebra
Solve for x:
In order to solve for x in a logarithmic function, we need to change it into exponential form. That looks as follows:
For this problem, manipulate the log and solve:
Example Question #72 : College Algebra
Solve for x:
In order to solve for x in a logarithmic function, we need to change it into exponential form. That looks as follows:
For this problem, manipulate the log and solve:
Example Question #73 : College Algebra
Solve for x:
In order to solve for x in a logarithmic function, we need to change it into exponential form. That looks as follows:
For this problem, manipulate the log and solve:
Example Question #25 : Solving Logarithmic Functions
What is the correct value of 
Divide by three on both sides.
If we would recall 
Cube both sides to isolate b.
The answer is:
Example Question #74 : College Algebra
What is the value of 
The expression can be rewritten as:
The answer is:
Example Question #75 : College Algebra
Solve this logarithm:
None of these
By the one-to-one property of logarithms we are able to set 
Example Question #76 : Exponential And Logarithmic Functions
Solve the logarithm:
add 8 to both sides:
divide both sides by -3:
exponentiate both sides:
Example Question #76 : College Algebra
On the day of a child's birth, a sum of money is to be invested into a certificate of deposit (CD) that draws 
If the amount of money invested is to be a multiple of 
If we let 
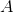
Substitute 
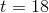
The minimum principal to be invested initially is $6,551. However, since we are looking for the multiple of $1,000 that guarantees a minimum final balance of $20,000, we round up to the nearest such multiple, which is $7,000 - the correct response.
Example Question #77 : College Algebra
Twelve years ago, your grandma put money into a savings account for you that earns 
$21,170
$81,030
$10,778
$24,596
$8,103
$24,596
1. Use 
2. Solve for
You currently have $24,596 in your account.
Example Question #78 : College Algebra
Jeffrey has won a lottery and has elected to take a $10,000 per month payment.
At the beginning of the year, Jeffrey deposits the first payment of $10,000 in an account that pays 7.6% interest annually, compounded continuously. At the very beginning of each month, he deposits another $10,000. How much will he have at the very end of the year?
The continuous compound interest formula is
where 
We can go ahead and calculate 
The formula can be rewritten as
At the beginning of January, Jeffrey deposits $10,000. At the end of January, there is
in the account.
At the beginning of February, he again deposits $10,000, so there is now
in the account.
At the end of February, there is
in the account.
Repeat addition of $10,000, then multiplication by 1.006353, ten more times to get the amount of money in the account at the end of December. This will be $125,072.98.
All College Algebra Resources
